Class 9 Hindi Naitik Siksha BSEH Solution for Chapter 7 गणित गौरव ब्रह्मगुप्त Explain for Haryana board. CCL Chapter Provide Class 1th to 12th all Subjects Solution With Notes, Question Answer, Summary and Important Questions. Class 9 Hindi mcq, summary, Important Question Answer, Textual Question Answer, Word meaning, Vyakhya are available of नैतिक शिक्षा Book for HBSE.
Also Read – HBSE Class 9 नैतिक शिक्षा Solution
Also Read – HBSE Class 9 नैतिक शिक्षा Solution in Videos
HBSE Class 9 Naitik Siksha Chapter 7 गणित गौरव ब्रह्मगुप्त / Ganit Gaurav Brhamgupt Explain for Haryana Board of नैतिक शिक्षा Class 9th Book Solution.
गणित गौरव ब्रह्मगुप्त Class 9 Naitik Siksha Chapter 7 Explain
महान ज्योतिषी और गणितज्ञ ब्रह्मगुप्त का जन्म 598 ई० अर्थात् 520 शक संवत् (655 वि०सं०) में हुआ था। इनका जन्म स्थान भिनमाल, माउण्ट आबू राजस्थान में है। यह स्थान गुजरात राज्य की सीमा से लगा हुआ है। ब्रह्मगुप्त के पिता का नाम विष्णुगुप्त था। ब्रह्मगुप्त उज्जैन गुरुकुल (वर्तमान मध्यप्रदेश) के प्रमुख खगोलशास्त्री थे।
ब्रह्मगुप्त ने ज्योतिषशास्त्र के दो प्रसिद्ध ग्रन्थों- ‘ब्रह्मस्फुट -सिद्धान्त’ और ‘खण्ड खाद्य’ की रचना की थी। ब्रह्मस्फुटसिद्धान्त की रचना 30 वर्ष की आयु में सन 628 ई. में की थी। ब्रह्मगुप्त से पूर्व भी ब्रह्म- सिद्धान्त’ नामक ग्रन्थ लिखा जा चुका था, किन्तु उसकी बातें न स्पष्ट थीं और न ही नवीन ज्ञान पर आधारित थीं। इसीलिए ब्रह्मगुप्त ने नया सिद्धान्त ग्रन्थ लिखा ब्रह्मस्फुटसिद्धान्त । ‘स्फुट’ का अर्थ है, फैलाया हुआ अथवा संशोधित । यह ग्रन्थ भारतीय खगोल शास्त्र का प्रामाणिक एवं मानक ग्रन्थ है। इस ग्रन्थ में 25 अध्याय और 1008 श्लोक हैं। इसके 12वें अध्याय को गणिताध्याय नाम दिया है अर्थात् इसमें अंकगणित तथा क्षेत्रमिति सम्बन्धी विषयों पर सामग्री दी गई है। इसके 18वें अध्याय को कुट्टकाध्याय नाम दिया है, इसमें बीजगणित, अनिर्धार्य रैखिक एवं वर्ग समीकरणों के हल दिए हैं। इसके अध्याय 2 में त्रिकोणमिति पर कार्य किया गया है। ब्रह्मगुप्त ने गणित विषय के अध्यायों में अंकगणित के सभी प्रक्रमों का ज्ञान दिया है। यही नहीं, उन्होंने गणित विषय से सम्बन्धित शून्य के उपयोग के नियम खोजे। इसी कारण भारतीय गणितज्ञों में सर्वप्रथम आर्यभट्ट उसके बाद भास्कराचार्य प्रथम, तत्पश्चात् ब्रह्मगुप्त का नाम विशेष सम्मान के साथ लिया जाता है। ब्रह्मगुप्त पहले गणितज्ञ थे, जिन्होंने गणित ज्योतिष की रचना विशेष क्रम से की और ज्योतिष तथा गणित को अलग-अलग अध्यायों में बाँटा ।
ब्रह्मगुप्त के ग्रन्थ की सबसे महत्त्वपूर्ण विशेषता है- बीजगणित उन्होंने बीजगणित को कुट्टक की संज्ञा दी है। ब्रह्मगुप्त ने समीकरणों के नए हल सुझाए। वेग का मान 10 मानकर चले हैं। उन्होंने न केवल वर्गीकरण की विधि का वर्णन सर्वप्रथम किया बल्कि विलोम विधि का भी सटीक और विस्तृत वर्णन किया है। ब्रह्मगुप्त ने अपने ग्रन्थ में 24 प्रकार के प्रश्नों के हल प्रस्तुत किए हैं। इनमें जोड़ना, घटाना, त्रैराशिक भाण्ड, प्रति भाण्ड, श्रोणी व्यवहार, क्षेत्र व्यवहार, त्रिभुज, चतुर्भुज आदि के क्षेत्रफल जानने की रीति, चित्र व्यवहार (ढाल, खाई आदि के घनफल जानने की रीति) त्रैवाचिक व्यवहार, राशि व्यवहार (अन्न के ढेर का परिमाण जानने की रीति) छाया व्यवहार (इसमें दोष सम्बन्ध तथा उसके स्तम्भ की अनेक रीतियाँ) आदि हैं।
ब्रह्मगुप्त का दूसरा महत्त्वपूर्ण ग्रन्थ है ‘खण्ड – खाद्य’। इसकी रचना उन्होंने सन 665 ई0 में की थी। इस ग्रन्थ में विशेषकर अन्तर्वेशन तथा समतल त्रिकोणमिति एवं गोलीय त्रिकोणमिति दोनों में (ज्या) और (कोटिज्या) के नियम उपलब्ध हैं। ब्रह्मगुप्त के दोनों ग्रन्थ भाण्डारकार प्राच्य विद्या संशोधन मन्दिर, पुणे, महाराष्ट्र में देखे जा सकते हैं। ब्रह्मगुप्त के इन दोनों ग्रन्थों का अनुवाद अरबी भाषा में ‘सिन्द हिन्द’ और ‘अलठ-अरकन्द’ नामक ग्रन्थों के रूप में किया गया। इस प्रकार इनकी प्रसिद्धि अरब देशों तक पहुँची और वे भारतीय गणित तथा ज्योतिष से लाभान्वित हुए। बाद में अंग्रेज विद्वान कोलबुक ने सन 1817 में कुट्टकाध्याय अर्थात् बीजगणित का अंग्रेजी भाषा में अनुवाद किया। तब पाश्चात्य विद्वानों को पता चला कि आधुनिक बीजगणित वास्तव में भारतीय बीजगणित पर आधारित है। उन्होंने गणित के क्षेत्र में-
- वर्गमूल तथा घनमूल ज्ञात करने की सरल विधियाँ दी हैं।
शून्य के गुणधर्म की व्याख्या करते हुए उसे एक अलग अंक के रूप में उल्लेखित किया। शून्य के उपयोग के नियम खोजे ।
ब्रह्मस्फुट सिद्धान्त के अध्याय 12 श्लोक संख्या 44 में उन्होंने वर्ग समीकरण के मूल ज्ञात करने की विधि दी है, जो इस प्रकार है-
वर्गचतुर्गुणितानां रूपाणां मध्यवर्गसहितानाम् ।
मूलं मध्येनोनं वर्गद्विगुणोधृतं मध्यः ।।
वर्तमान में प्रचलित सूत्र तथा इस विधि में समानता है।
- इसी प्रकार इन्होंने त्रिभुज तथा चक्रीय चतुर्भुज के क्षेत्रफल ज्ञात करने की विधि बताते हुए लिखा है-
स्थूलफलं त्रिचतुर्भुजबाहू प्रतिबाहुयोग दसघातः भुजयोगार्धचतुष्टय भुजोनघातात् पदं सूक्ष्मम्।।
भुजाओं के योग के आधे को चार बार लिखकर भुजाएँ घटाएँ। इन्हें गुणा कर वर्गमूल निकालें ।
चक्रीय चतुर्भुज का क्षेत्रफल = √(s-a) (s-b)(s-c) (s-d)
जहाँ a, b, c एवं d चक्रीय चतुर्भुज की भुजाएँ हैं तथा 2s = a+b+c+d है। =
त्रिभुज का क्षेत्रफल = √(s (s-a) (s-b)(s-c) तथा 2s= a+b+c
यह सूत्र ब्रह्मगुप्त प्रमेय के नाम से प्रसिद्ध है, जो यूरोप में प्रथम बार डब्लू स्नैल ने (1619 ई.) में अपने एक ग्रन्थ की टीका में दिया।
- चक्रीय चतुर्भुज की भुजाएँ ज्ञात होने पर उसके कणों की लम्बाइयाँ ज्ञात करने का उन्होंने निम्नलिखित सूत्र दिया है-
कर्णाश्रित भुज घाततैक्यमुभयथान्योन्यभाजितं गुणयेत् । योगेन भुजप्रतिभुजवधयोः कर्णौ पदे विषमे ।
यदि a, b, c एवं d चक्रीय चतुर्भुज की भुजाएँ हों तो
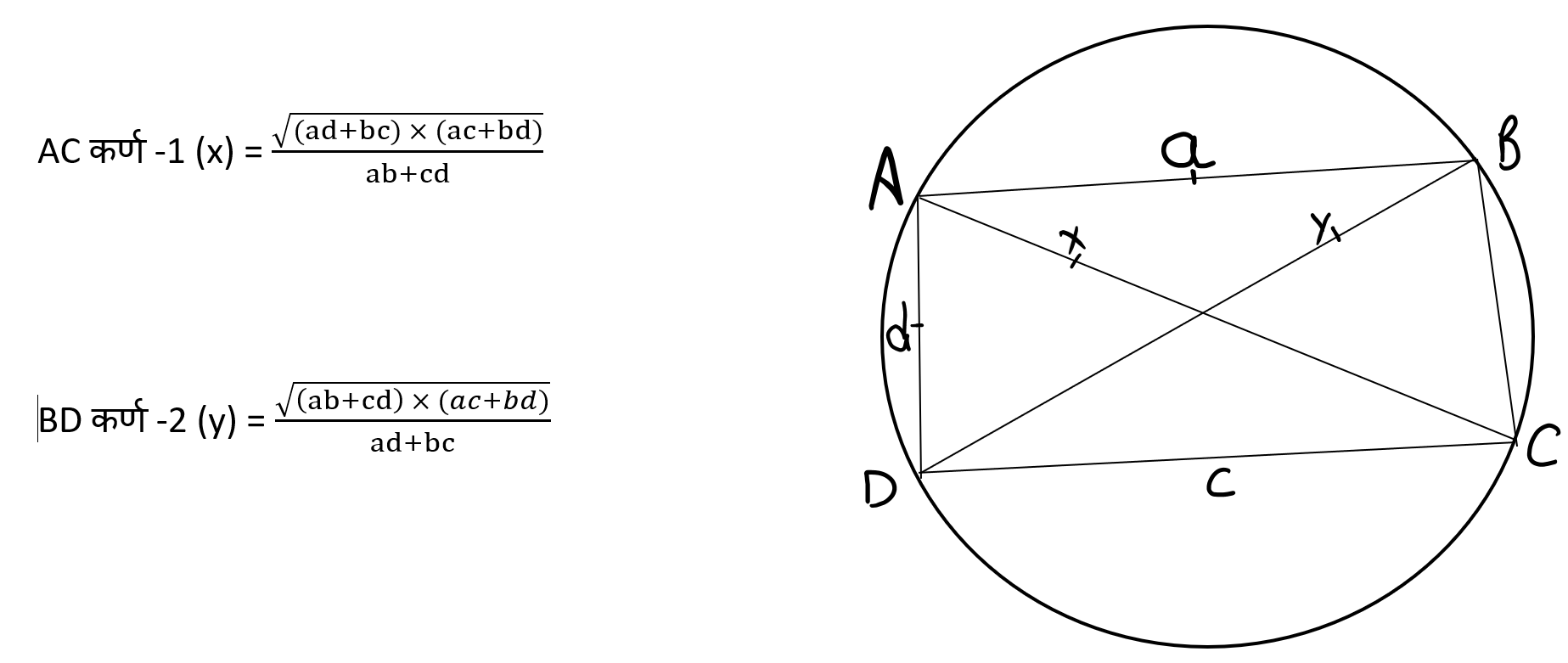
आधुनिक गणित के एक इतिहासवेत्ता हावार्ड ईव्स के शब्दों में कर्ण की लम्बाई ज्ञात करने के ये सूत्र भारतीय ज्यामिति के सबसे विलक्षण और उत्तमता में अनुपम हैं। गणित के क्षेत्र में उनके महत्त्वपूर्ण योगदान को देखकर प्रसिद्ध ज्योतिषी एवं गणितज्ञ भास्कराचार्य ने उन्हें ‘गणक चक्र चूड़ामणि’ नाम से सम्मानित किया। पाश्चात्य जगत में अनिवार्य वर्ग-समीकरण का श्रेय जॉन पेल (1688 ई०) को है किन्तु भारत में ब्रह्मगुप्त उनसे एक हजार वर्ष पहले अनिवार्य वर्ग-समीकरण-अय² + 1 = र² का हल प्रस्तुत कर चुके थे।
गणित में नई खोज करने के लिए ब्रह्मगुप्त हमारे लिए प्ररेणास्रोत तो हैं ही, अनुकरणीय भी हैं। इस महान गणितज्ञ की मृत्यु 680 ई० में हुई थी।