Class 11 Physics BSEH Solution for all Chapters Important Question Answer for Haryana board. CCL Chapter Provide Class 1th to 12th all Subjects Solution With Notes, Question Answer, Summary and Important Questions.
Also Read – HBSE Class 11 Important Questions in Videos 2024
Also Read – HBSE Class 11 Important Questions
HBSE Class 11 Physics Important Question Answer / grade 11 physics Important questions of all chapters Solution.
HBSE Class 11 Physics Important Questions With Answer 2024
Table of Contents
Class 11 Physics Chapter 1 Units and Measurements Important Questions 2024
Q1. What is unit of work in C.G.S. system?
Q2. What is SI unit of Gas Constant ?
Q3. ________ is defined as the mass of a Platinum-Iridium cylinder kept in Paris.
Q4. If a physical quantity is P = a2b2/c2 and the percentage errors in the measurements of a, b and c are 1%, 2% and 3% respectively, find the maximum percentage error in the measurement of physical quantity P.
Q5. If a physical quantity is X = a³b³/c and the percentage errors in the measurement of a, b and c are 1%, 2% and 3% respectively. Find the maximum percentage error in the measurement of physical quantity X.
Q6. In a relation F = a + bx where F is the force, x is the distance. Calculate dimensions of a and b.
Q7. If a physical quantity is and the percentage errors in measurement of a, b and c are 1%, 2% 3% respectively. Find the maximum percentage error in the measurement and of physical quantity X.
Q8. What will be the ratio of fundamental frequencies of an open and closed organ pipe of same length?
Class 11 Physics Chapter 2 Motion in a Straight line Important Questions 2024
Q1. Define uniformly accelerated motion. A particle is moving with uniform acceleration a in a straight path. Its initial velocity is u, displacement S and final velocity v. Using calculus method show that: v² = u² + 2aS
Q2. Obtain equation of motion S = ut + 1/2 at² for constant acceleration using method of calculus. S = displacement, u = initial velocity, t = time.
Q3. Check the equation v = u + at by the method of dimensions. Where v = Final velocity, u = Initial velocity, a = Acceleration, t = Time. Most Important
Q4. An object is moving in a given direction with a definite velocity. Draw time-velocity and time-displacement graphs for the object.
Q5. An object is moving with a constant acceleration. Draw time-velocity and time displacement graphs for the object.
Q6. Define uniformly accelerated motion. A particle is moving with uniform acceleration a in a straight path. Its initial velocity is u and final velocity v after time t. Using calculus method show that .
Q7. A man walks 4m East, then 5 m North, then taking a right turn walks 8 m straight. Calculate the distance travelled by the man and its displacement.
Class 11 Physics Chapter 3 Motion in a Plane Important Questions 2024
Q1. What are scalar and vector quantities? Give examples. Find the magnitude and direction of the resultant of two vectors and
in terms of their magnitudes and angle θ between them. Also define parallelogram law of vector addition.
Q2. If two vectors and
represent two adjacent sides of parallelogram, then prove that, magnitude of resultant R =
Where A and B respectively, magnitude of
and
and θ is the angle between them.
Q3. If two vectors and
represent two adjacent of parallelogram, then prove that, sides of magnitude of resultant R =
and Direction of resultant with
is
Where A and B respectively, magnitude of and
and θ is the angle between them.
Q4. Write parallelogram law of vector addition.
Q5. The angle of projection for which a projectile cover the maximum horizontal range is _________.
Q6. The angles of projection for which a projectile covers the same horizontal range, are 30° and _________.
Q7. A projectile is thrown at an angle θ from the horizontal with velocity u under the gravitational field of Earth. Find expression for time of flight.
Q8. A projectile is thrown at an angle θ from the horizontal with velocity u under the gravitational field of earth. Find its maximum height attained and the horizontal range. Most Important
Q9. A projectile is thrown at an angle from the horizontal with velocity u under the gravitational field of Earth. Find expression for Time of flight and Horizontal Range.
Q10. What do you mean by projectile ? Prove that path of a projectile is parabolic. Find the expression for maximum Height of projectile, Time taken to reach this height and the horizontal rang.
Q11. What do you understand by the term projectile motion. If a projectile is projected at an angle θ from the horizontal with velocity u in the gravitational field, prove that the path of the projectile will be a parabola.
Q12. If a vector is multiplied by a scalar m, what will be the resultant vector?
Q13. Explain the motion of a vehicle on a level circular path and give the formula for maximum velocity.
Class 11 Physics Chapter 4 Laws of Motion Important Questions 2024
Q1. State Newton’s Second Law of Motion. Define S.I. unit of force.
Q2. What do you mean by Friction ? Write laws of friction.
Q3. What is relation between coefficient of static friction and the angle of friction? Most Important
Q4. A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 ms-1. If the mass of the ball is .15 kg, determine the impulse imparted to the ball. (Assume linear motion of the ball.)
Q5. What do you mean by impulse ? Is impulse a scalar or a vector quantity.
Q6. A cricketer moves his hands backwards while holding a catch. Why?
Q7. Give answers to the following questions –
(i) If the net force acting on a body be zero then will the body remain necessarily in ‘rest position.
(ii) Write second law of motion in vector form.
Q8. By using ball bearings, sliding friction can be converted into _________ friction. Most Important
Q9. Establish relation between coefficient of friction and angle of friction.
Q10. Write the Laws of Limiting friction. Most Important
Q11. What do you mean by conservative and non- conservative forces? Give one example of each.
Q12. The centripetal force F acting on a particle moving in circular orbit depends on its mass m, radius of the circle r and the speed of particle v. Obtain the formula for the centripetal force, using dimension method.
Q13. What do you understand by Centripetal Force ? A particle of mass m is moving in a circular orbit of radius r with uniform speed v. Write the formula and direction of Centripetal Force acting on the particle.
Q14. A particle is revolving in circular orbit in a horizontal plane. The centripetal force (F) acting on it depends upon the mass (m), radius (r) of the circle and speed (v) of the particle. Obtain the formula for the centripetal force on it by the method of dimensional analysis.
Class 11 Physics Chapter 5 Work, Energy and Power Important Questions 2024
Q1. Explain work-energy theorem.
Q2. What is potential energy? Find the expression for potential energy of a spring.
Q3. If on applying force F, body move with velocity v, then power will be ___________.
Q4. Show that mechanical energy of a freely falling body justifies the Law of Conservation of Mechanical Energy.
Q5. Work done by a person in lifting a bucket out of a well by means of a rope tied to the bucket is positive or negative ?
Q6. The rate of doing work by a machine is called ___________ of the machine.
Q7. A gas is carried through the path AB, BC and CA according to the adjoining figure. What is the net work done in the whole cycle?
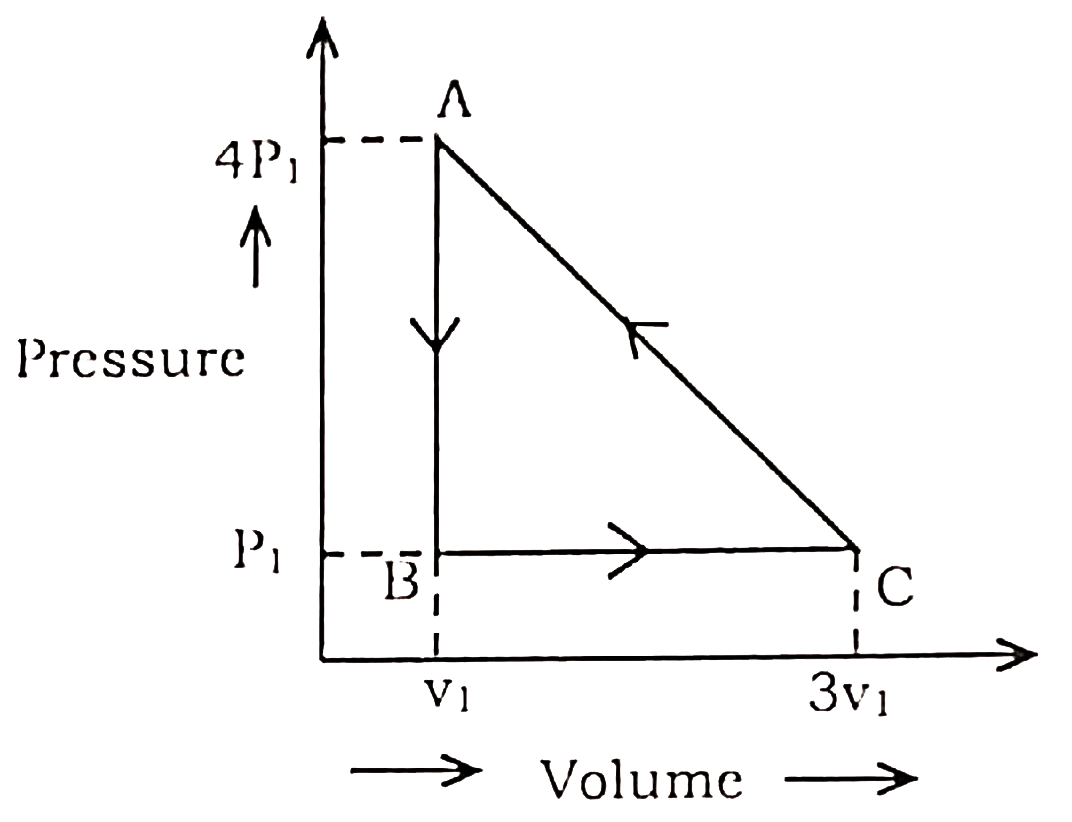
Q8. 4.18 Joule of work is equivalent to calories of heat.
Q9. The applied force = 3i + 4j – 5k on a particle produces displacement
= 5i + 4j + 3k. calculate work done by the force. Most Important
Q10. Write down the formula for work done in rotatory motion. Most Important
Q11. ________ Joule of work is equivalent to 1 calorie of heat.
Q12. The _______ of a body is defined as its capacity of doing work.
Q13. When 100 Joule of heat is given to a gaseous system, then internal energy increases by 30 Joule. Find the work done by the system. Most Important
Q14. An electric heater supplies heat to a system at a rate of 100 W. If system performs work at a rate of 75 joules per second. At what rate is the internal energy increasing?
Q15. When the momentum of body is increased by three times, its K.E becomes ___________.
Q16. How many erg are there in 1 Joule?
Class 11 Physics Chapter 6 System of Particles and Rotational Motion Important Questions 2024
Q1. What is meant by ‘centre of mass’ of a system ? Obtain expression for the centre of mass of a system consisting of two particles. Most Important
Q2. Obtain expression for the centre of mass of a system consisting of two a particles. Most Important
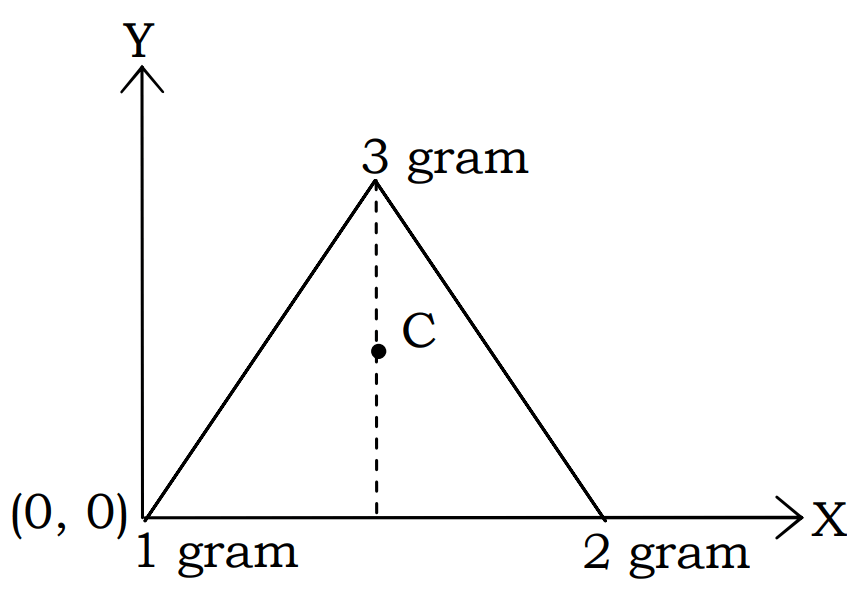
Q3. Locate the centre of mass of a system of three particles of masses 1 gram, 2 gram and 3 gram placed at the corners of an equilateral triangle of 1 meter side.
Q4. From a uniform disc of radius R, a circular disc of radius is cut out. The centre of the circular cut is at
from the centre of the 2 original disc. Locate the centre of mass of the resulting flat body.
Q5. State the Law of Conservation of Angular Momentum. Explain it by giving any one example. Most Important
Q6. Establish the relation between torque and moment of Inertia in rotational motion and define from it moment of Inertia.
Q7. State and prove theorem of perpendicular axis. Using this theorem find the moment of inertia of a disc about one of its diameters..
Q8. Find the torque of a force about the origin. The force acts on a particle whose position vector is
.
Class 11 Physics Chapter 7 Gravitation Important Questions 2024
Q1. What is the mathematical form of Kepler’s third law?
Q2. Define Escape speed. Find expression/formula for the Escape speed of earth.
Q3. Obtain the formula for the escape velocity of a body from the Earth. Most Important
Q4. In the universe each particle of matter attracts every other particle. This universal attractive force is called __________.
Q5. The average distance of the sun from a planet is four times in comparison to average distance of Sun from Earth. Find the time period of revolution of the planet.
Q6. Write the value of orbital velocity of Satellite revolving near the surface of Earth.
Q7. Define Gravitational Potential Energy.
Q8. Obtain the expression for acceleration due to gravity at depth d below the Earth’s surface, in terms of acceleration due to gravity at Earth’s surface and the radius of Earth.
Q9. What is a Geo-stationary Satellite. Write its one use.
Q10. Discuss the variation of acceleration due to gravity ‘g’ on going above the surface of earth.
Q11. If the earth revolves around the Sun in circular orbit, then what would be the work done by the gravitational force?
Q12. What is time-period of Geo-stationary satellite ? Most Important
Q13. Name and define the various absolute and gravitational units of force. How are these units related to each other?
Q14. Check weather mv² = mgh equation is dimensionally correct or not : Here m = mass of material, v = velocity, g = gravitational acceleration, h = height
Q15. A planet is revolving round the sun as shown in figure:
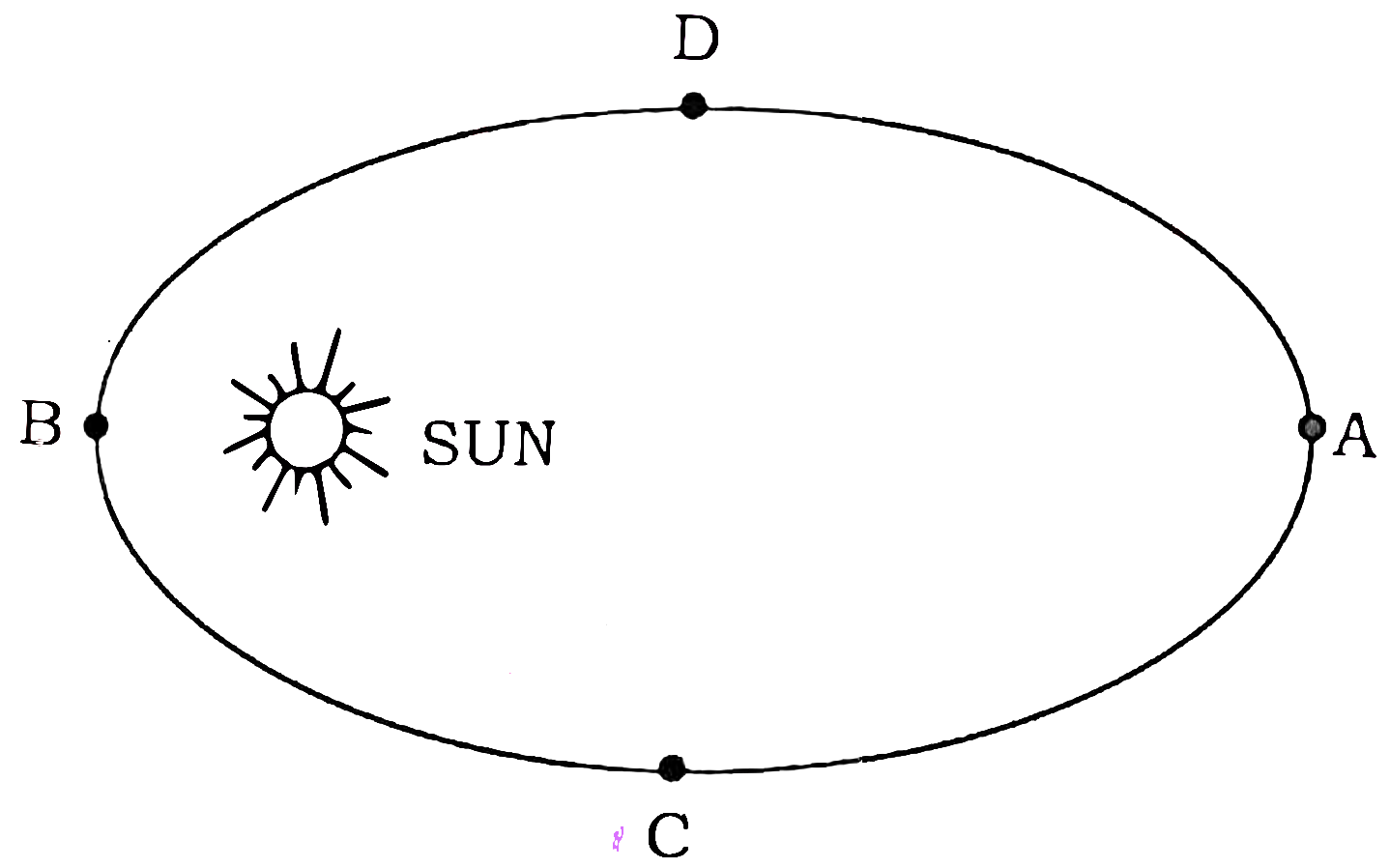
At which point the velocity of the planet is maximum ?
Q16. The value of ___________ is determined to be 6.67×10-11 Newton-metre2/kg2.
Q17. Why are high tides and low tides in the sea?
Class 11 Physics Chapter 8 Mechanical Properties of Solids Important Questions 2024
Q1. With help of stress-strain curve explain limit of elasticity, yield point.
Q2. The Young’s modulus of steel is greater than that of rubber. Give reason.
Q3. Write relation between coefficient of linear expansion (∝) and coefficient of surface expansion (β) of a solid material.
Q4. Write relation between coefficient of linear expansion (α) and coefficient of volume expansion (r) of a solid material.
Q5. Explain the meaning of the coefficient of linear expansion (α), coefficient of superficial expansion (β) and coefficient of volume expansion (γ) of a solid material. Establish relation among α and γ.
Q6. Establish relation between coefficient of linear expansion (α), coefficient of superficial expansion(β), and coefficient of volume expansion (γ).
Class 11 Physics Chapter 9 Mechanical Properties of Fluids Important Question 2024
Q1. State and prove Bernoulli’s theorem. Most Most Important
Q2. Define surface tension of a liquid. Find an expression for the access pressure inside a soap bubble.
Q3. A force of 160 N is applied on a nail, whose tip has a cross-sectional area of .004 cm². Calculate the pressure on the tip.
Q4. What is Viscosity ? What is the difference between Viscosity and friction ?
Q5. What do you mean by Viscosity ? Obtain an expression for terminal velocity of a ball falling in a viscous liquid.
Q6. By virtue of which property does the free surface of a liquid try to keep its area minimum ?
Q7. The angle inside the liquid between the tangent to the solid surface and the tangent to the liquid surface at the point of contact is called ________ for that pair of solid and liquid.
Q8. Derive expression for the formula of rise of water in a capillary tube.
Q9. Write Stoke’s Law.”
Q10. Define “coefficient of thermal conductivity” and write its unit.
Q11. What do you understand by capillarity ? Write down the formula for the rise of liquid in a capillary tube.
Class 11 Physics Chapter 10 Thermal Properties of Matter Important Questions 2024
Q1. State the Law of Equipartition of Energy. Prove that for an ideal gas r =1+ 2/f, where f is the number of degree of freedom of gas molecules.
Q2. What is the relation of internal energy of an ideal gas with gas temperature?
Q3. Analytically derive the formula for the work done by one mole of an ideal gas during isothermal expansion from volume V1 to volume V2.
Q4. What is adiabatic change? Write the relation between pressure and volume of an ideal gas for an adiabatic change. What is the meaning of r.
Q5. How many modes of heat transfer? Explain in details.
Q6. Write Newton’s Law of Cooling. Most Important
Q 7. State and prove Newton’s Law of Cooling. Most Important
Q8. What do you mean by specific heat capacity. Find the ratio of two specific heats Cp and Cv for diatomic gases. Cp = specific heat capacity at constant pressure, Cv = specific heat capacity at constant volume.
Class 11 Physics Chapter 11 Thermodynamics Important Questions 2024
Q1. Establish Mayer’s formula Cp – Cv = R from the First Law of Thermodynamics. Most Important
Q2. Explain, Second Law of thermodynamics with the help of suitable diagram. Most Important
Q3. Which thermodynamical variable is defined by the zeroth law of thermodynamics?
Q4. What is the First Law of thermodynamics ? Explain adiabatic process on the basis of first law of thermodynamics.
Q5. Which law of thermodynamics first introduced the concept of Internal Energy?
Q6. ___________ is 1/273.16 th part of thermodynamic temperature of the triple point of water.
Q7. Is coefficient of performance of a refrigerator constant ?
Q8. Give two examples of isothermal process.
Q9. Write two difference between Isothermal and Adiabatic process. Most Important
Q10. Explain the work done in an isothermal process and find formula for work.
Class 11 Physics Chapter 12 Kinetic Theory Important Questions 2024
Q1. How much will be the Kinetic Energy of a gas at the absolute zero? Most Important
Q2. Write down the postulates of kinetic theory of gases. Most Important
Q3. The number of degrees of freedom of a molecule of a diatomic gas is __________.
Q4. Write Pascal’s Law.
Class 11 Physics Chapter 13 Oscillations Important Questions 2024
Q1. The equation of a simple harmonic motion is y = 10sin100πt. Give value of amplitude of oscillation. Most Important
Q2. Derive expression of kinetic and potential energy of a single harmonic oscillator. Hence show that total mechanical energy, E = K + U easy constant in S.H.M.
Q3. Find expression for kinetic energy, potential energy and total energy of oscillation of a body executing simple harmonic motion.
Q4. Draw velocity-time graph of a particle executing simple harmonic motion.
Q5. Draw acceleration-time graph of a particle executing simple harmonic motion.
Q6. Write the formula of acceleration of a particle executing simple harmonic motion and draw its acceleration-time curve.
Q7. When a body being acted by an external periodic force, vibrates with the frequency of the force, then the vibrations of the body are called _________ vibrations. Most Important
Q8. Obtain an expression for the time-period of a simple pendulum.
Q9. What will be the value of the time period of a simple pendulum if the amplitude is reduced to half of its original value ?
Q10. What is simple pendulum? The bob of a simple pendulum has a mass of .025 kg. The effective length of the string is 1 metre and time period 2 second. Calculate the value of acceleration due to gravity (g).
Q11. What is Second’s Pendulum ? Determine its length.
Q12. A simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its fume period. Using method of dimensions.
Q13. In an experiment of simple pendulum, a student made several observations for the period of oscillations. His reading turned out to be : 2.63 sec, 2.56 sec, 2.42 sec, 2.71 sec and 2.80 sec. With the help of above observations calculate absolute errors and relative error.
Q14. A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork in depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period Where ρ is the density of cork (ignore damping due to viscosity of the liquid).
Q15. Discuss the formation of harmonics in stretched string. Show that in case of a stretched string the first four harmonics are in the ratio 1 : 2 : 3 : 4.
Q16. Find out the amplitude and the frequency from the equation of SHM y = 5 sin 100πt. The displacement has been expressed in meters and the time in seconds.
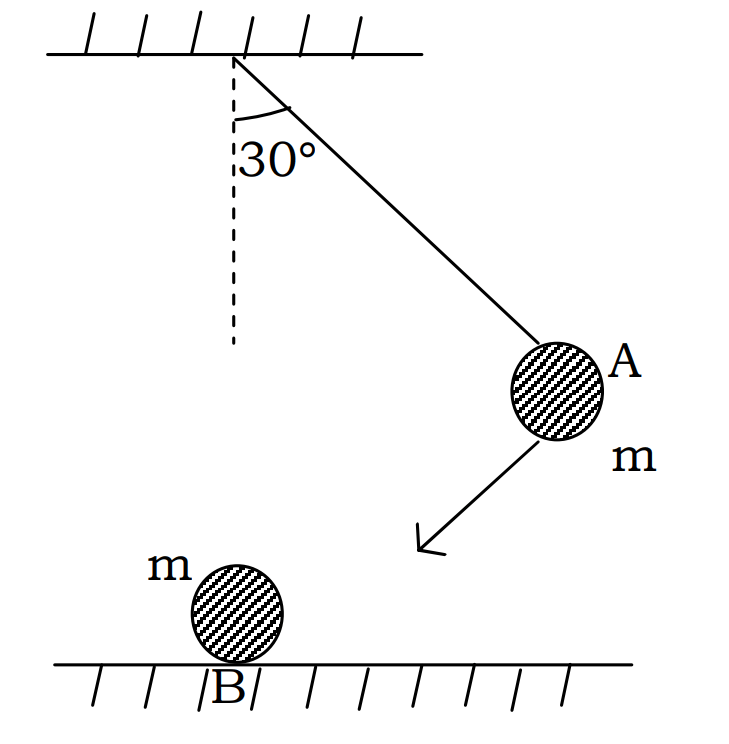
Q17. The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.
Class 11 Physics Chapter 14 Waves Important Questions 2024
Q1. Write laws of Transverse Vibrations of a Stretched String.
Q2. Define Standing waves and Beats.
Q3. Write down the formula for the speed of transverse waves in a stretched string.
Q4. What is meant by stationary wave ? Prove that in an open organ pipe, both odd and even harmonics are produced. Most Important
Q5. Prove that the number of beats heard per second is equal to the difference in frequencies of two sound sources. Most Important
Q6. When two sound sources are sounded together, then 2 beats are produced in .20 Second. Find the frequency of the beats.