NCERT Class 10 Math Chapter 10 Important Question Answer in Hindi – वृत्त

Class 10
Chapter  वृत्त
Subject गणित
Category Important Questions

Class 10 Math Chapter 10 Important Question Answer in Hindi

प्रश्न 1. बाह्य बिन्दु से वृत्त पर खींची गई स्पर्शरेखाओं की लम्बाइयाँ __________ होती हैं।

Ans – बराबर

प्रश्न 2. एक वृत्त की _________ समांतर स्पर्श रेखाएँ हो सकती हैं। Most Important

Ans – दो

प्रश्न 3. सभी वृत्त _________ होते हैं। (समरूप/सर्वांगसम) Most Important

Ans – समरूप

प्रश्न 4. किसी वृत्त की स्पर्श रेखा उसे _________बिन्दुओं पर  प्रतिच्छेद करती है।

Ans – एक

प्रश्न 5. वृत्त को दो बिन्दुओं पर प्रतिच्छेद करने वाली रेखा को ________ कहते हैं।

Ans – छेदक

प्रश्न 6. किसी वृत्त की स्पर्शरेखा उसे _________ बिन्दुओं पर प्रतिच्छेद करती है।

Ans – एक

प्रश्न 7. वृत्त तथा उसकी स्पर्श रेखा के उभ्यनिष्ठ बिंदु को _________ कहते हैं।

Ans – स्पर्श बिंदु

प्रश्न 8. एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 सेमी तथा Q की केन्द्र से दूरी 25 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।

Ans –

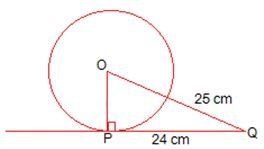
स्पर्श रेखा PQ की लंबाई = 24 सेमी

OQ = 25 सेमी

वृत्त OP की त्रिज्या = ?

जैसा कि हम जानते हैं, वृत्त पर किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु से गुजरने वाली त्रिज्या के लंबवत होती है

इसलिए, OT ⊥ PQ

∆ OPQ में, पाइथागोरस प्रमेय का उपयोग करने पर

OQ2 = OP2 + PQ2

252 = OP2 + 242

625 – 576 = 49 = OP2

OP = 7 सेमी

इसलिए, दिए गए वृत्त की त्रिज्या की लंबाई 7 सेमी है।

प्रश्न 9. एक बिन्दु से एक वृत्त पर स्पर्श रेखा की लम्बाई ज्ञात कीजिए जिसकी वृत्त के केन्द्र से दूरी 25 सेमी है। वृत्त की त्रिज्या 7 सेमी दी हुई है।

Ans –

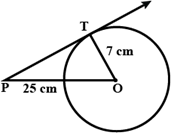
वृत्त OT की त्रिज्या = 7 cm

PO = 25 सेमी

PT = ?

जैसा कि हम जानते हैं, वृत्त पर किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु से गुजरने वाली त्रिज्या के लंबवत होती है

इसलिए, PT ⊥ OT

∆ PTO में, पाइथागोरस प्रमेय का उपयोग करने पर

PO2 = TO2 + PT2

252 = 72 + PT2

625 – 49 = 576 = PT2

PT = 24 सेमी

अतः स्पर्श रेखा की आवश्यक लंबाई 24 सेमी है।

प्रश्न 10. 5 सेमी त्रिज्या के वृत्त की 8 सेमी लम्बी एक जीवा PQ है। P और Q पर स्पर्श रेखाएँ परस्पर एक बिन्दु T पर प्रतिच्छेद करती हैं। TP की लम्बाई ज्ञात कीजिए, यदि वृत्त का केन्द्र O है।

Ans –

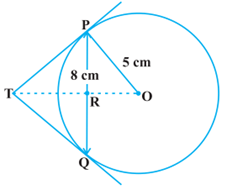
मान लीजिए OT रेखा PQ को बिंदु R पर प्रतिच्छेद करती है। तब ∆ TPQ समद्विबाहु है और TO का कोण ∠PTQ समद्विभाजक है। तो, OT⊥PQ और इसलिए, OT, PQ को समद्विभाजित करती है जिससे PR = RQ = 4 सेमी प्राप्त होता है।

इसके अलावा, OR = \displaystyle \sqrt{{O{{P}^{2}}-P{{R}^{2}}}}=\sqrt{{{{5}^{2}}-{{4}^{2}}}} = 3 सेमी

अब, ∠TPR + ∠RPO = 90° = ∠TPR + ∠PTR

∠RPO = ∠PTR

इसलिए, समकोण त्रिभुज TRP कोण-कोण समानता द्वारा समकोण त्रिभुज PRO के समान है।

\displaystyle \frac{{TP}}{{PO}}=\frac{{RP}}{{RO}}, अर्थात   \displaystyle \frac{{TP}}{5}=\frac{4}{3}  या TP = \displaystyle \frac{{20}}{3} सेमी

 

नोट: TP को पाइथागोरस प्रमेय का उपयोग करके भी पाया जा सकता है। (Alternate Choice for Attempt same Questions)

माना TP = x और TR = y.

पाइथागोरस प्रमेय का उपयोग करने पर

x2 = y2 + 16  (समकोण ∆ PRT उपयोग करने पर)  —— (i)

x2 + 52 = (y + 3)2 (समकोण ∆ OPT उपयोग करने पर)  —– (ii)

समीकरण (ii) से समीकरण (i) घटाने पर, हमें प्राप्त होता है

25 = 6y – 7

y = \displaystyle \frac{{32}}{6}=\frac{{16}}{3}

समीकरण (i) में y का मान रखने पर, हमें प्राप्त होता है

x2 = \displaystyle {{\left( {\frac{{16}}{3}} \right)}^{2}}+16=\frac{{16}}{9}\left( {16+9} \right)=\frac{{16\times 25}}{9}

x = \displaystyle \frac{{20}}{3} सेमी

प्रश्न 11. सिद्ध कीजिए कि किसी वृत्त के व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।

Ans –

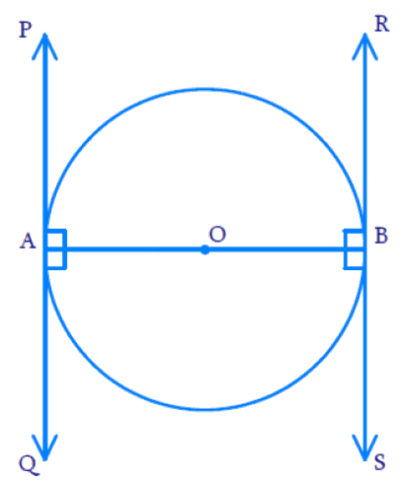
आइए केंद्र O और व्यास AB वाला एक वृत्त बनाएं।

मान लीजिए कि दो स्पर्श रेखाएं खींची गई हैं, एक बिंदु A पर PQ है और दूसरी बिंदु B पर RS खींची गई है।

जैसा कि हम जानते हैं,

OA ⊥ PQ (वृत्त पर किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु से गुजरने वाली त्रिज्या के लंबवत होती है)

∠OAP = 90° —– (i)

इसी प्रकार, OB ⊥ RS (वृत्त पर किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु से गुजरने वाली त्रिज्या के लंबवत होती है)

∠OBS = 90° —– (ii)

समीकरण (i) और (ii) से हम पाते हैं,

∠OAP = ∠OBS  = 90°

चूँकि, रेखा PQ और RS के लिए AB एक अनुप्रस्थ रेखा है और ∠BAP = ∠ABS है

यानी यदि एकांतर कोण बराबर हों तो रेखाएं समानांतर होती हैं।

इसलिए, PQ || RS

अत: सिद्ध हुआ।

प्रश्न 12. किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं, सिद्ध कीजिए। Most Most Important

Ans –

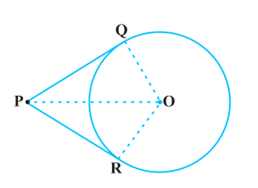
हमें केंद्र O वाला एक वृत्त, वृत्त के बाहर स्थित एक बिंदु P और P से वृत्त पर दो स्पर्शरेखाएँ PQ, PR दी गई हैं।

हमें यह सिद्ध करना है कि PQ = PR

इसके लिए हम OP, OQ और OR को जोड़ते हैं। तब ∠OQP और ∠ORP समकोण हैं, क्योंकि ये त्रिज्याओं और स्पर्श रेखाओं के बीच के कोण हैं, और वे समकोण हैं क्योंकि वृत्त के किसी भी बिंदु पर स्पर्शरेखा संपर्क बिंदु के माध्यम से त्रिज्या के लंबवत होती है।

अब समकोण त्रिभुज OQP और ORP में,

OQ = OR          (उसी वृत्त की त्रिज्या)

OP = OP            (Common)

इसलिए, OQP ≅ ORP  (RHS)

इससे मिलता है   PQ = PR   (सर्वांगसम त्रिभुज के संगत भाग)

प्रश्न 13. केन्द्र O वाले वृत्त पर बाह्य बिन्दु T से दो स्पर्श-रेखाएँ TP तथा TQ खींची गई हैं। सिद्ध कीजिए किं PTQ = 2 OPQ है।

Ans –

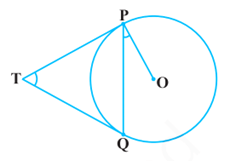
हमें केंद्र O वाला एक वृत्त, एक बाह्य बिंदु T और वृत्त की दो स्पर्श रेखाएँ TP और TQ दी गई हैं, जहाँ P, Q संपर्क बिंदु हैं।

हमें यह साबित करने की जरूरत है :

∠PTQ = 2∠OPQ

माना ∠PTQ= θ

अब, TP = TQ क्योंकि बाह्य पथ से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है।

तो, TPQ एक समद्विबाहु त्रिभुज है।

इसलिए, ∠TPQ = ∠TQP = \displaystyle \frac{1}{2}\left( {{{{180}}^{o}}-\theta } \right)={{90}^{o}}-\frac{1}{2}\theta

इसके अलावा,, ∠OPT = 90o क्योंकि वृत्त के किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु के माध्यम से त्रिज्या के लंबवत होती है।

इसलिए, ∠OPQ = ∠OPT – ∠TPQ = 90o – \displaystyle \left( {{{{90}}^{o}}-\frac{1}{2}\theta } \right)

= \displaystyle \frac{1}{2}\theta =\frac{1}{2}\angle PTQ

इससे ∠PTQ = 2 ∠OPQ प्राप्त होता है

प्रश्न 14. सिद्ध कीजिए कि दो संकेन्द्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर समद्विभाजित होती है।

Ans –

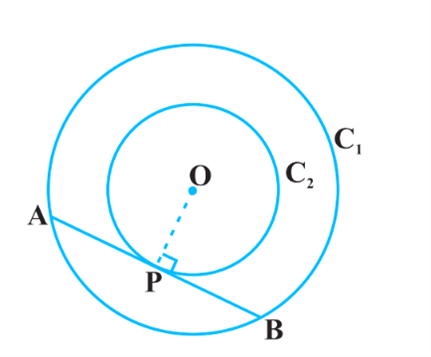
हमें दो संकेंद्रित वृत्त दिए गए हैं, C1 और C2 केंद्र O और बड़े वृत्त C1 की एक जीवा AB के साथ जो छोटे वृत्त C2 को बिंदु P पर स्पर्श करती है 

हमें यह सिद्ध करना होगा कि AP = BP.

आइए OP से जुड़ें।

फिर, AB, P पर C2 की स्पर्श रेखा है और OP इसकी त्रिज्या है। इसलिए, OP ⊥ AB

अब AB वृत्त C1 की एक जीवा है और OP ⊥ AB है। इसलिए, OP जीवा AB का समद्विभाजक है, क्योंकि केंद्र से लंब जीवा को समद्विभाजित करता है

यानी AP = BP

प्रश्न 15. दो संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमशः 5 सेमी तथा 3 सेमी हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।

Ans –

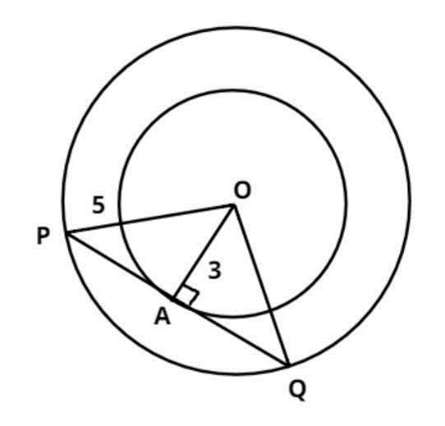
बड़े वृत्त की त्रिज्या OP = 5 cm

छोटे वृत्त की त्रिज्या OA = 3 cm

ज्ञात करना है PQ = ?

OA ⊥ PQ (क्योंकि वृत्त की त्रिज्या सदैव उसकी स्पर्श रेखा के लंबवत होती है)

साथ ही, PA = AQ (क्योंकि ∆ OAP ≅ ∆ OAQ)

∆ OAP में, पाइथागोरस प्रमेय का उपयोग करने पर

PO2 = PA2 + AO2

52 = PA2 + 42

9 = PA2

PA = 3

PQ = PA + AQ = 3 + 3 = 6cm

प्रश्न 16. सिद्ध कीजिए कि एक वृत्त की जीवा के सिरों पर खींची गयी स्पर्श रेखा जीवा से बराबर कोण बनाती है।

Ans –

दिया गया है: वृत्त के केंद्र O, PA और PB जीवा AB पर सिरों A और B पर खींची गई स्पर्श रेखाएं हैं।

सिद्ध: करना है ∠PAB = ∠PBA

प्रमाण: OA और OB को मिलाएँ।

OA = OB (समान वृत्त की त्रिज्या)

∠OAB = ∠OBA (समान भुजाओं के सम्मुख कोण) —– (i)

∠OAP = ∠OBP = 90 (चूंकि त्रिज्या हमेशा स्पर्श रेखा के लंबवत होती है)

∠OAB + ∠PAB = ∠OBA + ∠PBA  — (ii)

समीकरण  (i) का मान समीकरण (ii) में रखने पर हमें मिलता है,

∠OAB + ∠PAB = ∠OAB + ∠PBA

∠PAB =  ∠PBA

अत: सिद्ध हुआ।

 

Leave a Comment

error: