NCERT Class 10 Math Chapter 12 Important Question Answer in Hindi – पृष्ठीय क्षेत्रफल और आयतन

Class 10
Chapter  पृष्ठीय क्षेत्रफल और आयतन
Subject गणित
Category Important Questions

Class 10 Math Chapter 12 Important Question Answer in Hindi

प्रश्न 1. ऊँचाई 2.4 से.मी. और व्यास 1.4 से. मी. वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग से. मी.2 तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।

Ans –

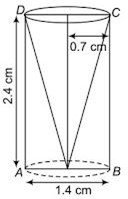
दिया गया है, बेलन की त्रिज्या r = \displaystyle \frac{{1.4}}{2}=0.7 सेमी,

बेलन की ऊँचाई, h = 2.4 सेमी

शंकु की त्रिज्या, r = 0.7 सेमी

शंकु की ऊँचाई, h = 2.4 सेमी

शंक्वाकार गुहा की तिरछी ऊंचाई (l) = \displaystyle \sqrt{{{{h}^{2}}+{{r}^{2}}}}

= \displaystyle \sqrt{{{{{(2.4)}}^{2}}+{{{(0.7)}}^{2}}}}=\sqrt{{5.76+0.49}}=\sqrt{{6.25}}

= 2.5 सेमी

शेष ठोस का कुल सतह क्षेत्रफल

= शंक्वाकार गुहा का सतह क्षेत्र + सिलेंडर की कुल तिरछी ऊंचाई

= πrl + 2πr(r + h)

= πr(l + 2h + r)

= \displaystyle \frac{{22}}{7}\times 0.7(2.5\times 4.8\times 0.7)

= 17.6 सेमी2

प्रश्न 2. दो घनों, जिनमें से प्रत्येक का आयतन 64 सेमी3 है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

Ans –

प्रत्येक घन का आयतन = 64 सेमी3

इसका मतलब है a3 = 64

a = 4 सेमी

अब, घन की भुजा a = 4 सेमी

साथ ही, परिणामी घनाभ की लंबाई 8 सेमी और चौड़ाई और ऊंचाई प्रत्येक 4 सेमी है।

इसलिए, परिणामी घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)

= 2(8×4 + 4×4 + 4×8)

= 2(32 + 16 + 32)

= 160 सेमी2

प्रश्न 3. कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का व्यास 14 सेमी है और इस बर्तन की कुल ऊँचाई 13 सेमी है। इस बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए। Most Important

Ans –

दिया गया है, अर्धगोले का व्यास = 14 सेमी

अत: गोलार्ध की त्रिज्या 7 सेमी होगी।

साथ ही, बेलन की ऊंचाई h = 13 – 7 = 6 सेमी

खोखले गोलार्ध की त्रिज्या = 7 सेमी

अब, बर्तन का आंतरिक सतह क्षेत्र = सिलेंडर का घुमावदार सतह क्षेत्र + गोलार्ध का घुमावदार सतह क्षेत्र

= 2πrh + 2πr2

= 2πr(h + r)

= \displaystyle 2\times \frac{{22}}{7}\times 7\left( {6+7} \right)

= 2×22×13

= 572 सेमी2

प्रश्न 4. एक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्द्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई 15.5 सेमी है। इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। Most Important

Ans –

दिया गया है, अर्धगोले की त्रिज्या = 3.5 सेमी

गोलार्द्ध का पृष्ठीय क्षेत्रफल = 2πr2

= \displaystyle 2\times \frac{{22}}{7}\times \frac{7}{2}\times \frac{7}{2} = 77 सेमी2

शंक्वाकार भाग की ऊँचाई = 15.5 सेमी – 3.5 सेमी = 12 सेमी

शंक्वाकार भाग की त्रिज्या = 3.5 सेमी

शंक्वाकार भाग की तिरछी ऊंचाई (l)  = \displaystyle \sqrt{{{{h}^{2}}+{{r}^{2}}}}

= \displaystyle \sqrt{{{{{12}}^{2}}+{{{3.5}}^{2}}}}=\sqrt{{144+12.25}}=\sqrt{{156.25}} = 12.5 सेमी

शंक्वाकार भाग का घुमावदार पृष्ठीय क्षेत्रफल = πrl = = 11×12.5 = 137.5 सेमी2

खिलौने का कुल पृष्ठीय क्षेत्रफल = गोलार्ध का पृष्ठीय क्षेत्रफल + शंक्वाकार भाग का पृष्ठीय क्षेत्रफल

= 77 सेमी2 + 137.5 सेमी2

= 214.5 सेमी2

प्रश्न 5. भुजा 7 सेमी वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है ? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

Ans –

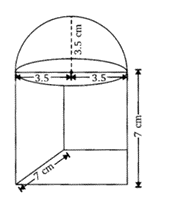
दिया गया है, घन की प्रत्येक भुजा = 7 सेमी

अत: गोलार्ध की त्रिज्या 7/2 सेमी होगी।

ठोस की कुल सतह = घन का कुल सतह क्षेत्र + गोलार्ध का घुमावदार सतह क्षेत्र – गोलार्ध के आधार का क्षेत्रफल

= 6(side)2 + 2πr2 – πr2

= 6(side)2 + πr2

= 6(7)2 + \displaystyle \frac{{22}}{7}\times \frac{7}{2}\times \frac{7}{2}

= 294 + \displaystyle \frac{{77}}{2}

= 294 + 38.5 = 332.5 सेमी2

 = 7 सेमी

प्रश्न 6. एक दवा कैप्सूल एक सिलेंडर के आकार का होता है जिसके प्रत्येक सिरे पर दो गोलार्ध लगे होते हैं। पूरे कैप्सूल की लंबाई 14 मिमी और कैप्सूल का व्यास 5 मिमी है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

Ans –

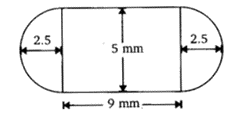
दिया गया है, कैप्सूल का व्यास = 5 मिमी

इसलिए, कैप्सूल की त्रिज्या = 5/2 = 2.5 मिमी

कैप्सूल की लंबाई = 14 mm

सिलेंडर की लंबाई = 14 – (2.5 + 2.5) = 9 मिमी

अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr2 = \displaystyle 2\times \frac{{22}}{7}\times \frac{5}{2}\times \frac{5}{2} = \displaystyle \frac{{275}}{7} मिमी2

अब, सिलेंडर का घुमावदार सतह क्षेत्र= 2πrh = \displaystyle 2\times \frac{{22}}{7}\times \frac{5}{2}\times 9=\frac{{990}}{7} मिमी2

दवा कैप्सूल का आवश्यक सतह क्षेत्र = 2 (गोलार्द्ध का सतह क्षेत्र) + सिलेंडर का घुमावदार सतह क्षेत्र

= \displaystyle 2\left( {\frac{{275}}{7}} \right)+\frac{{990}}{7}=\frac{{1540}}{7}=220 मिमी2

प्रश्न 7. एक बेलन के वक्र पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र लिखिए।

Ans –

बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh

जहां r आधार की त्रिज्या है और h सिलेंडर की ऊंचाई है।

 = 2πrh

प्रश्न 8. जमीन के नीचे पानी का एक तालाब है जो कि घनाभ के आकार का है, जिसकी भुजाएँ 48 मी, 36 मी एवं 28 मी हैं। इसका आयतन ज्ञात कीजिए।

Ans –

घनाकार पानी की टंकी के आयाम 48 मीटर, 36 मीटर और 28 मीटर हैं।

इसलिए,

घनाकार टैंक का आयतन = lbh

= 48 × 36 × 28

= 48,384 मीटर3

प्रश्न 9. 21 सेमी की ऊँचाई तथा 5 सेमी आधार की त्रिज्या वाले लम्ब बेलन का आयतन __________ है।

Ans –

दिया गया है r = 5 सेमी, h = 21 सेमी

लंबवृत्तीय शंकु का आयतन = πr2h

= \displaystyle \frac{{22}}{7}\times 5\times 5\times 21

= 1650 सेमी2

प्रश्न 10. 24 सेमी की ऊँचाई और 6 सेमी आधार त्रिज्या वाले शंकु का आयतन ज्ञात कीजिए।

Ans –

दिया गया है r = 6 सेमी and h = 24 सेमी

शंकु का आयतन = \displaystyle \frac{1}{3}πr2h

= \displaystyle \frac{1}{3}× \displaystyle \frac{{22}}{7}×6×6×24 = \displaystyle \frac{{6336}}{7} सेमी3

इसलिए, शंकु का आवश्यक आयतन है \displaystyle \frac{{6336}}{7} सेमी3

प्रश्न 11. त्रिज्या 8 सेमी० वाले गोले का आयतन _________ है।

Ans –

गोले की त्रिज्या r = 8 सेमी

गोले का आयतन = \displaystyle \frac{4}{3}πr3 = \displaystyle \frac{4}{3}× \displaystyle \frac{{22}}{7}×8×8×8 = \displaystyle \frac{{45056}}{{21}} सेमी3

 

Leave a Comment