NCERT Class 10 Math Chapter 12 Important Questions Answer – Surface Areas and Volumes

Class 10
Chapter  Surface Areas and Volumes
Subject Math
Category Important Question Answer

Class 10 Math Chapter 12 Important Question Answer

Q1. From a solid cylinder whose height is 2.4cm and diameter 1.4cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.

Ans.

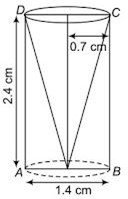
Given, Radius of cylinder r = \displaystyle \frac{{1.4}}{2}=0.7 cm,

Height of cylinder, h = 2.4 cm

Radius of cone, r = 0.7 cm

Height of cone, h = 2.4 cm

Slant height of the conical cavity (l) = \displaystyle \sqrt{{{{h}^{2}}+{{r}^{2}}}}

= \displaystyle \sqrt{{{{{(2.4)}}^{2}}+{{{(0.7)}}^{2}}}}=\sqrt{{5.76+0.49}}=\sqrt{{6.25}}

= 2.5 cm

Total surface are of the remaining solid

= Surface area of conical cavity + TSA of the cylinder

= πrl + 2πr(r + h)

= πr(l + 2h + r)

= \displaystyle \frac{{22}}{7}\times 0.7(2.5\times 4.8\times 0.7)

= 17.6 cm2

Q2. Two cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid. Most Important

Ans.

Volume of each cube = 64 cm3

It means a3 = 64

a = 4 cm

Now, the side of cube, a = 4 cm

Also, the length of resulting cuboid is 8 cm and breadth and height is 4 cm each.

Therefore, the surface area of resulting cuboid = 2(lb + bh + hl)

= 2(8×4 + 4×4 + 4×8)

= 2(32 + 16 + 32)

= 160 cm2

Q3. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and total height of the vessel is 13 cm. Find the inner surface area of the vessel.

Ans.

Given, diameter of hemisphere = 14cm

Therefore, radius of hemisphere will be 7 cm.

Also, height of the cylinder, h = 13 – 7 = 6 cm

Radius of the hollow hemisphere = 7 cm

Now, The Inner surface area of the vessel = CSA of the cylinder + CSA of Hemisphere

= 2πrh + 2πr2

= 2πr(h + r)

= \displaystyle 2\times \frac{{22}}{7}\times 7\left( {6+7} \right)

= 2×22×13

= 572 cm2

Q4. A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Ans.

Given, radius of hemisphere = 3.5 cm

Surface area of the hemisphere = 2πr2

= \displaystyle 2\times \frac{{22}}{7}\times \frac{7}{2}\times \frac{7}{2} = 77 cm2

Height of conical part = 15.5 cm – 3.5 cm = 12 cm

Radius of conical part = 3.5 cm

Slant height of conical part (l)  = \displaystyle \sqrt{{{{h}^{2}}+{{r}^{2}}}}

= \displaystyle \sqrt{{{{{12}}^{2}}+{{{3.5}}^{2}}}}=\sqrt{{144+12.25}}=\sqrt{{156.25}} = 12.5 cm

Curved surface area of conical part = πrl = = 11×12.5 = 137.5 cm2

Total surface area of the toy = Surface area of hemisphere + Surface area of conical part

= 77 cm2 + 137.5 cm2

= 214.5 cm2

Q5. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have ? Find the surface area of solid.

Ans.

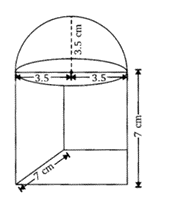
Given, each side of cube = 7 cm. So, the radius of hemisphere will be 7/2 cm.

Total surface of the solid

= Total Surface area of cube + CSA of hemisphere – Area of base of hemisphere

= 6(side)2 + 2πr2 – πr2

= 6(side)2 + πr2

= 6(7)2 + \displaystyle \frac{{22}}{7}\times \frac{7}{2}\times \frac{7}{2}

= 294 + \displaystyle \frac{{77}}{2}

= 294 + 38.5 = 332.5 cm2

Q6. A medicine capsule is in the shape of a cylinder with two hemisphere struck to each of its ends. The length of entire capsule is 14 mm and diameters of the capsule is 5 mm. Find its surface area.

Ans.

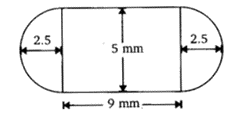
Given, diameter of capsule = 5 mm.

Therefore, radius of capsule = 5/2 = 2.5 mm

Length of the capsule = 14 mm

Length of the cylinder = 14 – (2.5 + 2.5) = 9 mm

Curved Surface area of a hemisphere = 2πr2 = \displaystyle 2\times \frac{{22}}{7}\times \frac{5}{2}\times \frac{5}{2} = \displaystyle \frac{{275}}{7} mm2

Now, the Curved surface area of cylinder = 2πrh = \displaystyle 2\times \frac{{22}}{7}\times \frac{5}{2}\times 9=\frac{{990}}{7} mm2

The required surface area of the medicine capsule = 2(surface area of hemisphere) + curved surface area of cylinder

= \displaystyle 2\left( {\frac{{275}}{7}} \right)+\frac{{990}}{7}=\frac{{1540}}{7}=220 mm2

Q7. Write the formula for finding out the curved surface area of the cylinder.

Ans. Curved surface area of cylinder = 2πrh

where r is the radius of base and h  is the height of cylinder.

Q8. An underground water tank is in the form of a cuboid of edges 48 m, 36 m and 28m. Find the volume of the tank.

Ans. Dimensions of cuboidal water tank are 48m, 36m  and 28m.

Therefore,

Volume of cuboid tank = lbh

= 48 × 36 × 28

= 48,384 m3

Q9. The volume of the right circular cone of height 21 cm and radius of its base 5 cm, is, _________.

Ans. Given r = 5 cm, h = 21 cm

Volume of right circular cone = πr2h

= \displaystyle \frac{{22}}{7}\times 5\times 5\times 21

= 1650 cm2

Q10. Find the volume of the cone of height 24 cm and radius of base 6 cm.

 Ans. Given r = 6 cm and h = 24 cm

Using,  Volume of Cone = \displaystyle \frac{1}{3}πr2h

= \displaystyle \frac{1}{3}× \displaystyle \frac{{22}}{7}×6×6×24 = \displaystyle \frac{{6336}}{7} cm3

Therefore, required volume of cone  is \displaystyle \frac{{6336}}{7} cm3

Q11. The volume of the sphere of radius 8 cm is _________.

Ans. radius of sphere r = 8 cm

Volume of sphere = \displaystyle \frac{4}{3}πr3 = \displaystyle \frac{4}{3}× \displaystyle \frac{{22}}{7}×8×8×8 = \displaystyle \frac{{45056}}{{21}} cm3

Also Read Class 10 Math NCERT Solution
Also Read Class 10 Important Questions [Latest]

Leave a Comment

error: