CCL Chapter

NCERT Class 10 Math Chapter 13 Important Question Answer in Hindi – सांख्यिकी

What's inside !!!

Class10
Chapter सांख्यिकी
Subjectगणित
CategoryImportant Questions

Class 10 Math Chapter 13 Important Question Answer in Hindi

प्रश्न 1. एक टेलीफोन निर्देशिका से 100 कुलनाम (surnames) लिए गए। उनमें प्रयुक्त अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारंबारता बंटन प्राप्त हुआ : Most Important

अक्षरो की संख्या1-44-77-1010-1313-1616-19
कुलनामों की संख्या630401644

कुलनामों के माध्यक अक्षरों की संख्या ज्ञात कीजिए।

Ans –

अक्षरो की संख्याकुलनामों की संख्यासंचयी बारंबारता
1-4

 

4-7

 

7-10

 

10-13

 

13-16

 

16-19

6

 

30

 

40

 

16

 

4

 

4

6

 

36

 

76

 

92

 

96

 

100

अब, n=100, \displaystyle \frac{n}{2}=\frac{{100}}{2}=50. यह अवलोकन वर्ग 7-10 में है।

तब, l (निम्न सीमा) = 7,

संचयी बारंबारता (कक्षा 7-10 से पहले वाले वर्ग की संचयी बारंबारता) = 36

बारंबारता (7-10 से पहले वाले वर्ग का माध्यक ) = 40,

h (वर्ग का आकार) = 3.

सूत्र का उपयोग करते हुए, माध्यक = l + \displaystyle \left( {\frac{{\frac{n}{2}-cf}}{f}} \right) × h

माध्यक =7 + \displaystyle \left( {\frac{{50-36}}{{40}}} \right)\times 3 =7  + 1.05 = 9.05

प्रश्न 2. निम्नलिखित ऑकड़ो का माध्यक 28.5 है। यदि बारंबारताओ का योग 60 है तो x और y का मान ज्ञात कीजिए : Most Important

वर्ग अंतराल0-1010-2020-3030-4040-5050-60
बारंबारता5x2015y5

Ans –

वर्ग अंतरालबारंबारतासंचयी बारंबारता
0-10

 

10-20

 

20-30

 

30-40

 

40-50

 

50-60

 

5

 

x

 

20

 

15

 

y

 

5

5

 

5 + x

 

25 + x

 

40 + x

 

40 + x + y

 

45 + x + y

यह दिया गया है कि n = 60

तो, 45 + x + y = 60  यानी, x + y = 15

माध्यक 28.5 है, जो वर्ग 20-30 में स्थित है

तो, l = 20,  f = 20,  cf = 5 + x,  h = 10

सूत्र का उपयोग करते हुए, माध्यक = l + \displaystyle \left( {\frac{{\frac{n}{2}-cf}}{f}} \right) × h

28.5 = 20 + \displaystyle \left( {\frac{{30-5-x}}{{20}}} \right)\times 10

28.5  – 20 = \displaystyle \frac{{25-x}}{2}

17 = 25 – x

x = 8

x + y = 15 में x का मान रखने पर,

हमें y = 7 प्राप्त होता है

प्रश्न 3. किसी फैक्टरी के 50 श्रमिकों की दैनिक मजदूरी के निम्नलिखित बंटन पर विचार कीजिए :

दैनिक मजदूरी (रुपयों में)100-120 120-140140-160160-180180-200
श्रमिकों की संख्या12148610

एक उपयुक्त विधि का प्रयोग करते हुए, इस फैक्टरी के श्रमिकों की माध्य दैनिक मजदूरी ज्ञात कीजिए।

Ans –

चूँकि दिया गया डेटा बड़ा है, हम माध्य ज्ञात करने के लिए पग-विचलन विधि का उपयोग करेंगे।

यहाँ a = 150, h = 20  

वर्ग अन्तरालबारंबारता (fi)वर्ग चिह्न (ui) \displaystyle {{u}_{i}}=\frac{{{{x}_{i}}-a}}{h}fiui
100-120

120-140

140-160

160-180

180-200

12

14

8

6

10

110

130

150 (a)

170

190

-2

-1

0

1

2

 

-24

-14

0

6

20

\displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}}}=50 \displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}}}{{u}_{i}}=-12

पग-विचलन विधि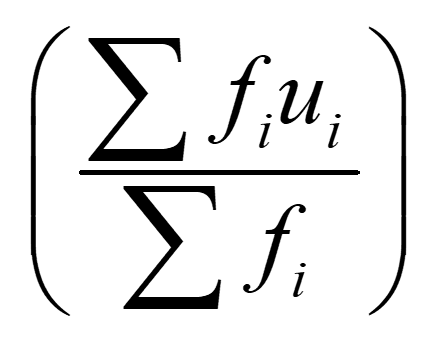 = \displaystyle \overline{x} = a + × h

= 150 + \displaystyle 20\left( {\frac{{-12}}{{50}}} \right) = 150 – \displaystyle \frac{{240}}{{50}}

= 145.20

अतः, भोजन पर औसत दैनिक व्यय 145.20 रुपये है

प्रश्न 4. निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेब खर्च को दर्शाता है। माध्य जेब खर्च Rs.18 है। लुप्त बारंबारता f ज्ञात कीजिए। Most Important

दैनिक जेबखर्च (₹ में)11-1213-1515-1717-1919-2121-2323-25
बच्चों की संख्या76913f54

Ans –

दैनिक जेबखर्च (₹ में)वर्ग चिन्ह (xi)बच्चों की संख्या (fi)Di = xi – 18fidi
11-13

13-15

15-17

17-19

19-21

21-23

23-25

12

14

16

18 ( माना a = 18)

20

22

24

7

6

9

13

f

5

4

-6

-4

-2

0

2

4

6

-42

-24

-18

0

2f

20

24

Total \displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}=44+f}} \displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}{{d}_{i}}=2f-40}}

हमारे पास है,

कल्पित माध्य विधि =  \displaystyle \overline{x} = a +

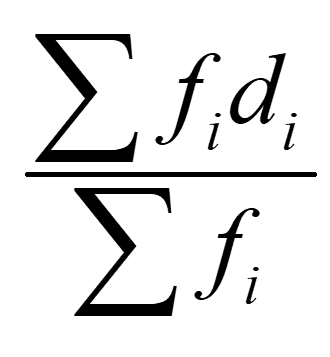
18 = 18 + \displaystyle \frac{{2f-40}}{{44+f}}

0 = \displaystyle \frac{{2f-40}}{{44+f}}

2f – 40 = 0

f = 20

इसलिए, लुप्त बारंबारता 20 है।

प्रश्न 5. निम्नलिखित आँकड़े 75 बिजली उपकरणों के प्रेक्षित जीवनकाल (घंटों में) की सूचना देते हैं : Most Important

जीवनकाल (घंटों में)0-2020-4040-6060-8080-100100-120
बारंबारता1015122189

उपकरणों का माध्य जीवनकाल ज्ञात कीजिए।

Ans –

यहां अधिकतम बारंबारता 21 है। अतः बहुलक वर्ग 60-80 है।

अब,

बहुलक वर्ग = 60-80, बहुलक वर्ग की निचली सीमा (l) = 60, वर्ग आकार (h) = 20

बहुलक वर्ग की बारंबारता (f1) = 21

बहुलक वर्ग से पहले वाले वर्ग की बारंबारता (f0) = 12,

बहुलक वर्ग के बाद वाले वर्ग की बारंबारता (f2) = 8

अब, बहुलक = l + 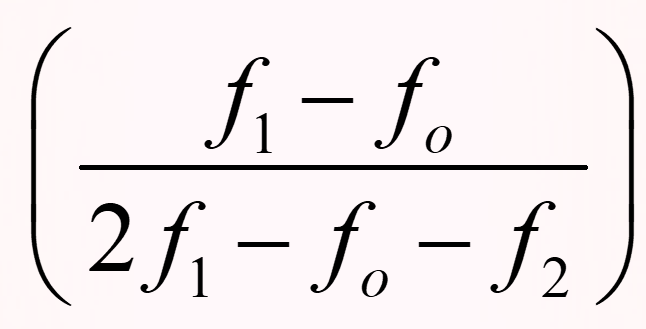× h का उपयोग करने पर

Mode = 60 + \displaystyle \left( {\frac{{21-12}}{{2(21)-12-8}}} \right)\times 20 = 60 + \displaystyle \frac{{90}}{{11}}= 68.18

प्रश्न 6. निम्नलिखित आँकड़ों की मध्यिका 525 है। x और y का मान ज्ञात कीजिए, यदि कुल बारंबारता 100 है :

वर्ग- अन्तरालबारंबारता
0-100

100-200

200-300

300-400

400-500

500-600

600-700

700-800

800-900

900-1000

2

5

x

12

17

20

y

9

7

4

Ans –

वर्ग- अन्तरालबारंबारतासंचयी बारंबारता
0-100

 

100-200

 

200-300

 

300-400

 

400-500

 

500-600

 

600-700

 

700-800

 

800-900

 

900-1000

2

 

5

 

x

 

12

 

17

 

20

 

y

 

9

 

7

 

4

2

 

7

 

7+x

 

19 + x

 

36 + x

 

56 + x

 

56 + x + y

 

65 + x + y

 

72 + x + y

 

76 + x + y

 

 यह दिया गया है कि n = 100

तो, 76 + x + y = 100  यानी, x + y = 24

माध्यक 525 है, जो वर्ग 500-600 में स्थित है

तो, l = 500,  f = 20,  cf = 36 + x,  h = 100

सूत्र का उपयोग करते हुए, माध्यक = l + \displaystyle \left( {\frac{{\frac{n}{2}-cf}}{f}} \right) × h

525 = 500 + \displaystyle \left( {\frac{{50-36-x}}{{20}}} \right)\times 100

525 – 500 = (14 – x)×5

25 = 70 – 5x

5x = 70 – 25 = 45

x = 9

x + y = 24 में x का मान रखने पर,

हमें 9 + y = 24 प्राप्त होता है

y = 15

प्रश्न 7. किसी स्कूल की कक्षा X की 51 लड़कियों की ऊँचाइयों का एक सर्वेक्षण किया गया और निम्नलिखित आँकड़े प्राप्त किए गए :

ऊँचाई (सेमी में)140 से कम145 से कम150 से कम155 से कम160 से कम165 से कम
लड़कियों की संख्या41129404651

माध्यक ऊँचाई ज्ञात कीजिए।

Ans –

दिया गया वितरण निम्न प्रकार का है। अत: वर्ग 140, 140-145, 145-150, ….., 160-165 से नीचे होने चाहिए।

140 से नीचे वर्ग अंतराल की बारंबारता 4 है, वर्ग अंतराल 140-145 की बारंबारता 11-4=7 है। इसी प्रकार 145-150 की बारंबारता 29-11=18 इत्यादि है।

तो, दी गई संचयी बारंबारता के साथ हमारी बारंबारता वितरण तालिका बन जाती है:

वर्ग- अन्तरालबारंबारतासंचयी बारंबारता (cf)
140 से कम44
140-145711
145-1501829
150-1551140
155-160646
160-165551

अब, n=51, \displaystyle \frac{n}{2}=\frac{{51}}{2}=25.5. यह प्रेक्षण अंतराल 145-150 में निहित है।

l (निम्न सीमा) = 145,

संचयी बारंबारता (145-150 से पहले वाले वर्ग की संचयी बारंबारता) = 11

f (माध्यक वर्ग की आवृत्ति 145-150) = 18,

h (वर्ग आकार) = 5

सूत्र का उपयोग करते हुए, माध्यक = l + \displaystyle \left( {\frac{{\frac{n}{2}-cf}}{f}} \right) × h

माध्यक = 145 + \displaystyle \left( {\frac{{25.5-11}}{{18}}} \right)\times 5

= 145 + \displaystyle \frac{{72.5}}{{18}} = 149.03

प्रश्न 8. किसी मोहल्ले के 25 परिवारों का भोजन पर व्यय निम्नलिखित है। भोजन पर हुआ माध्य व्यय ज्ञात कीजिए : Most Important

खर्च (₹ में)100-150150-200200-250250-300200-350
परिवारों की संख्या451222

Ans –

यहाँ, a = 225 और h = 50

वर्ग- अन्तरालबारंबारतावर्ग चिन्ह \displaystyle {{u}_{i}}=\frac{{{{x}_{i}}-a}}{h}fiui
100-150

150-200

200-250

250-300

300-350

4

5

12

2

2

125

175

225 (a)

275

325

-2

-1

0

1

2

 

-8

-5

0

2

4

\displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}}}=25 \displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}}}{{u}_{i}}=-7

पग-विचलन विधि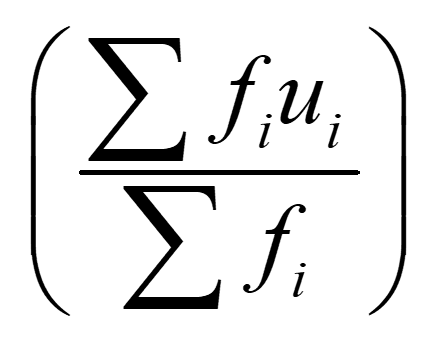 = \displaystyle \overline{x} = a + × h

= 225 + \displaystyle 50\left( {\frac{{-7}}{{25}}} \right) = 225 – 14

= 211.

अतः भोजन पर औसत दैनिक व्यय 211 रुपये है।

प्रश्न 9. निम्नलिखित सारणी में एक स्कूल के विद्यार्थियों का दैनिक जेब खर्च दिया गया है : Most Important

दैनिक जेब खर्च (₹ में)11-1313-1515-1717-1919-2121-2323-25
विद्यार्थियों की संख्या769132054

इस स्कूल के बच्चों का औसत जेब खर्च ज्ञात कीजिए।

Ans –

दैनिक जेब खर्च (₹ में)वर्ग चिन्ह (xi)विद्यार्थियों की संख्या (fi)Di = xi – 18fidi
11-13

13-15

15-17

17-19

19-21

21-23

23-25

12

14

16

18 ( let a = 18)

20

22

24

7

6

9

13

20

5

4

-6

-4

-2

0

2

4

6

-42

-24

-18

0

40

20

24

कुल \displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}=64}} \displaystyle \sum\limits_{{}}^{{}}{{{{f}_{i}}{{d}_{i}}=0}}

 

हमारे पास है,

कल्पित माध्य विधि = \displaystyle \overline{x} = a +

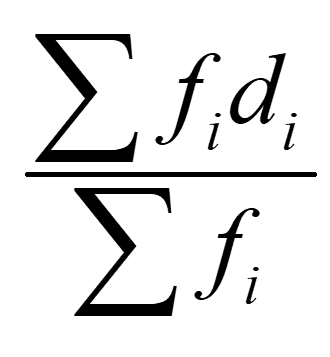
\displaystyle \overline{x} = 18 + \displaystyle \frac{0}{{64}} = 18

इसलिए,स्कूल के बच्चों का औसत जेब 18 ₹ है

प्रश्न 10. निम्नलिखित बारंबारता बंटन किसी मोहल्ले के बिजली की मासिक खपत दर्शाता है। इस बंटन का माध्यक ज्ञात कीजिए :

मासिक खपत (इकाइयों में)65-8585-105105-125125-145145-165165-185
उपभोक्ताओं की संख्या451320144

Ans –

मासिक खपत (इकाइयों में)उपभोक्ताओं की संख्या (f)संचयी बारंबारता (cf)
65-8544
85-105812
105-1251325
125-1452045
145-1651459
165-185463

अब, n = 63, \displaystyle \frac{n}{2}=\frac{{63}}{2}=31.5. यह प्रेक्षण अंतराल 125-145 में निहित है।

l (निम्न सीमा) = 125,

संचयी बारंबारता (125-145 से पहले वाले वर्ग की संचयी बारंबारता) = 25,

f (माध्यक वर्ग की आवृत्ति 125-145) = 20,

h (वर्ग आकार) = 20.

सूत्र का उपयोग करते हुए, माध्यक = l + \displaystyle \left( {\frac{{\frac{n}{2}-cf}}{f}} \right) × h

माध्यक = 125 + \displaystyle \left( {\frac{{31.5-25}}{{20}}} \right)20 = 125 + 6.5 = 126.5

प्रश्न 11. किसी गेंदबाज द्वारा 10 क्रिकेट मैचों में लिए गए विकेटों की संख्याएँ निम्नलिखित हैं
3    5     2    1     2     0    5     1     2     4
इनका बहुलक ज्ञात कीजिए।

Ans –

डेटा को आरोही क्रम में व्यवस्थित करने पर : 0, 1, 2, 2, 2, 3, 4, 5, 5

From above data we can clearly conclude that 3 is the mode of data as it is used in max times.

उपरोक्त डेटा से हम स्पष्ट रूप से यह निष्कर्ष निकाल सकते हैं कि 3 डेटा का बहुलक है क्योंकि इसका उपयोग अधिकतम समय में किया जाता है।

इसलिए, बहुलक = 3

 

Copyright © 2025 CCL Chapter