NCERT Class 10 Math Chapter 3 Important Question Answer in Hindi – दो चर वाले रैखिक समीकरण युग्म

Class 10
Chapter  दो चर वाले रैखिक समीकरण युग्म
Subject गणित
Category Important Questions

Class 10 Math Chapter 3 Important Question Answer in Hindi

प्रश्न 1. निम्न रैखिक समीकरणों के युग्म को हल कीजिए: 2x + 3y = 7 और 6x – 5y = 11.

Ans –

हमें दिया गया हैं

2x + 3y = 7    —- (i)

6x – 5y = 11   —- (ii)

चरण 1 : समीकरण (i) को 5 से तथा समीकरण (ii) को 3 से, y के गुणांकों को समान करने के लिए, गुणा करिए। तब हम निम्न समीकरण पाते हैंः

10x + 15y = 35

18x – 15y = 33

चरण 2 : दोनों समीकरणों को जोड़ने पर, हमें प्राप्त होगा :

28x = 68

x = \displaystyle \frac{{68}}{{28}}=\frac{{17}}{7}

चरण 3 : समीकरण (i) में x का मान प्रतिस्थापित करने पर, हमें मिलता है

2 \displaystyle \left( {\frac{{17}}{7}} \right)  + 3y = 7

3y = \displaystyle 7-\frac{{34}}{7}=\frac{{49-34}}{7}=\frac{{15}}{7}

y = \displaystyle \frac{5}{7}

समीकरणों के युग्म का हल  है :  x = \displaystyle \frac{{17}}{7}, y = \displaystyle \frac{5}{7}

[ नोट : आप किसी भी समीकरण में x और y का मान डालकर इसे सत्यापित कर सकते हैं। ]

प्रश्न 2. k के किस मान के लिए निम्नलिखित रैखिक समीकरण युग्म में अनंत संख्या में समाधान हैं? (k – 1)x + (k + 1)y = 3k – 1 और 2x + 3y = 7

Ans –

यहां a1 = k – 1, a2 = 2, b1 = k + 1, b2 = 3, c1 = 3k – 1, c2 = 7

अब दिए गए युग्म के लिए अनंत संख्या में समाधान हैं:

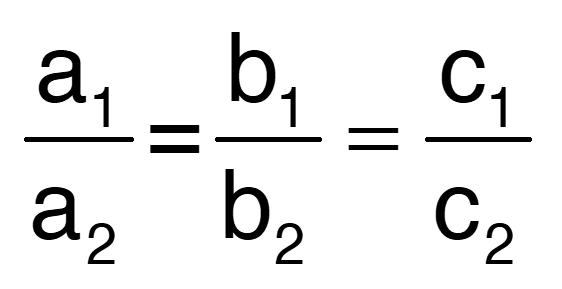
\displaystyle \frac{{k-1}}{2}=\frac{{k+1}}{3}=\frac{{3k-1}}{7}

(i) और (ii) की तुलना करने पर हमें मिलता है,

\displaystyle \frac{{k-1}}{2}=\frac{{k+1}}{3}

3k – 3 = 2k + 2

k = 5

इसलिए, k = 5 के लिए, समीकरण युग्म में अनंत संख्या में समाधान होंगे।

प्रश्न 3. रैखिक समीकरण 3x + 5y = 7 और 9x – 10y = 14 का युग्म संगत है या असंगत

Ans – यहां a1= 3, a2 = 9, b1 = 5, b2 = -10, c1 = 7, c2 = 14

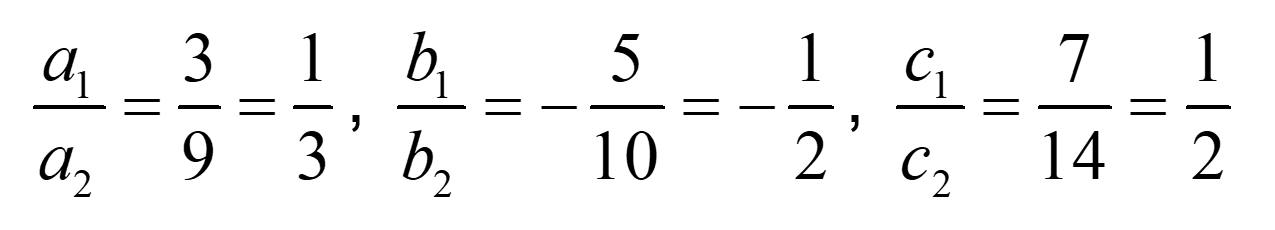
ऊपर समीकरण युग्म से यह स्पष्ट है कि

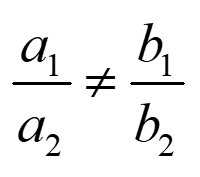
इसलिए, रैखिक समीकरण का युग्म संगत है।

प्रश्न 4. K के किन मानों के लिए, निम्न रैखिक समीकरणों के युग्म का एक अद्वितीय हल है ? 4x + Ky + 8 = 0 तथा 2x + 2y + 2 = 0

Ans – यहां a1= 4, a2 = 2, b1 = k, b2 = 2 

अब दिए गए समीकरण युग्म के लिए एक अद्वितीय हल प्राप्त करना है:

\displaystyle \frac{4}{2}\ne \frac{k}{2}

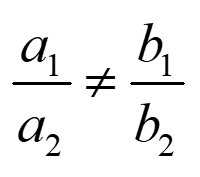
k≠4

इसलिए, 4 को छोड़कर, k के सभी मानों के लिए, दिए गए समीकरण युग्म का एक अद्वितीय हल होगा।

प्रश्न 5. K के किन मानों के लिए, निम्न रैखिक समीकरणों के युग्म का कोई हल नहीं होगा ?  x – ky + 4 = 0 तथा 2x – 6y – 5 = 0

Ans – यहां a1= 1, a2 = 2, b1 = -k, b2 = -6, c1 = 4, c2 = -5

अब दिए गए युग्म का कोई हल नहीं है:

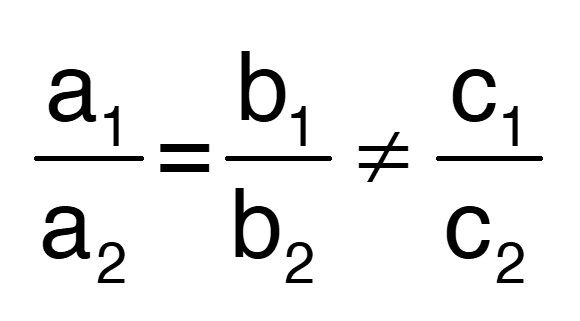
\displaystyle \frac{1}{2}=\frac{{-k}}{{-6}}\ne \frac{4}{{(-5)}}

यानी \displaystyle \frac{1}{2}=\frac{k}{6}

k = 3

इसलिए, k = 3 के लिए, दिए गए समीकरण युग्म का कोई हल नहीं होगा।

प्रश्न 6. x + y = 5 और 2x – 3y = 4 को हल कीजिए।

Ans –

x + y = 5  —- (i)

2x – 3y = 4 —— (ii)

समीकरण (i) को 3 से गुणा करने पर हमें 3x + 3y = 15 प्राप्त होता है

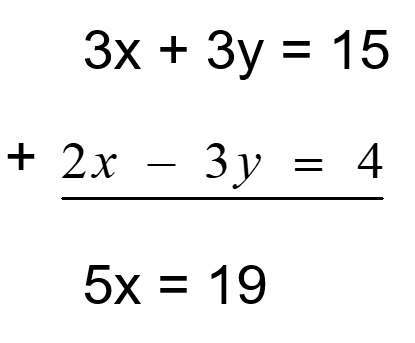
x = \displaystyle \frac{{19}}{5}

समीकरण (i) में x का मान रखने पर, \displaystyle \frac{{19}}{5} + y = 5

Y = 5 – \displaystyle \frac{{19}}{5} = \displaystyle \frac{6}{5}

प्रश्न 7. यदि हम अंश में एक जोड़ दें और हर में से एक घटा दें तो भिन्न एक में बदल जाती है। यदि हर में एक जोड़ दे तो वह \displaystyle \frac{1}{2} हो जाती है। वह भिन्न क्या है ?

Ans –

माना अंश = x है

माना हर = y है

इसलिए, भिन्न = \displaystyle \frac{x}{y}

पहली स्थिति के अनुसार,

\displaystyle \frac{{x+1}}{{y-1}}=1

x + 1 = y – 1

x – y = -2  —- (i)

दूसरी स्थिति के अनुसार,

\displaystyle \frac{x}{{y+1}}=\frac{1}{2}

2x = y + 1

2x – y = 1 —- (ii)

समीकरण (ii) से समीकरण (i) घटाने पर हमें मिलता है,

x = 3

समीकरण (i) में x का मान रखने पर हमें प्राप्त होता है,

3 – y = -2

Y = 5

इसलिए, भिन्न  \displaystyle \frac{3}{5} है।

प्रश्न 8. पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुना हो जायेगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या है ?

Ans –

माना जैकब की आयु x वर्ष है।

साथ ही, माना कि उसके पुत्र की आयु y वर्ष है।

प्रश्न के अनुसार,

(x + 5) = 3(y + 5)

x – 3y = 10 ——- (i)

(x – 5) = 7(y – 5)

x – 7y = -30 —— (ii)

समीकरण (ii) को (i) से घटाने पर हमें मिलता है,

4y = 40

y = 10

समीकरण (i) में y का मान प्रतिस्थापित करने पर हमें मिलता है,

x = 40

अतः जैकब की वर्तमान आयु 40 वर्ष है और उसके पुत्र की वर्तमान आयु 10 वर्ष है।

प्रश्न 9. पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष पश्चात् नूरी की आयु सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की वर्तमान आयु कितनी है ?

Ans –

माना नूरी की आयु x वर्ष है।

साथ ही, माना सोनू की आयु y वर्ष है।

प्रश्न के अनुसार,

(x – 5) = 3(y – 5)

x – 3y = -10  ——- (i)

x + 10 = 2(y + 10)

x – 2y = 10  ——- (ii)

समीकरण (i) को (ii) से घटाने पर हमें मिलता है,

y = 20

समीकरण (i) में y का मान प्रतिस्थापित करने पर हमें मिलता है,

x – 3(20) = -10

x = -10 + 60

x = 50

अतः नूरी की आयु 50 वर्ष और सोनू की आयु 20 वर्ष है।

प्रश्न 10. दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। वह संख्या ज्ञात कीजिए ।

Ans –

माना किसी संख्या का इकाई अंक x है।

साथ ही, मान लीजिए कि किसी संख्या का दहाई अंक y है।

फिर, संख्या n = 10y + x

अंकों का क्रम उलटने पर संख्या = 10x + y

प्रश्न के अनुसार,

x + y = 9  —- (i)

9(10y + x) = 2(10x + y)

88y – 11x = 0

8y – x = 0  —— (ii)

समीकरण (i) और (ii) जोड़ने पर हमें प्राप्त होता है

9y = 9

y = 1

समीकरण (i) में y का मान रखने पर हमें प्राप्त होता है

x = 8

अतः संख्या 18 है।

 

Leave a Comment

error: