| Class | 10 |
| Chapter | त्रिभुज |
| Subject | गणित |
| Category | Important Questions |
Class 10 Math Chapter 6 Important Question Answer in Hindi
प्रश्न 1. भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि उनके संगत कोण _________ हो। (बराबर, समानुपाती)
Ans – बराबर
प्रश्न 2. यदि दो समरूप त्रिभुजो के क्षेत्रफल बराबर हो तो सिद्ध कीजिए कि वे सर्वागसम होते हैं।
Ans –
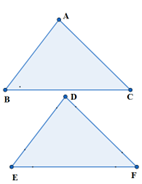
आइए ∆ ABC ~ ∆ DEF लें। जैसा कि हम जानते हैं, समरूप त्रिभुजों में संगत कोण और संगत भुजाएँ बराबर होती हैं। तो, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F और संगत भुजाओं का अनुपात
=
=
हम इस प्रमेय को जानते हैं कि यदि दो त्रिभुज समरूप हैं, तो दोनों त्रिभुजों के क्षेत्रफल का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के समानुपाती होता है। तो हमारे पास
=
=
=
प्रश्न में हमें दिया गया है कि ∆ ABC का क्षेत्रफल = ∆ DEF का क्षेत्रफल। तो हमारे पास,
=
=
=
1 = =
=
हल करने पर हमें मिलता है,
1 =
दोनों तरफ वर्गमूल करने पर हमें मिलता है
1 =
AB = DE,
इसी प्रकार, 1 = यानी BC = EF
और 1 = यानी CA = FD
चूँकि त्रिभुजों की संगत भुजाओं की लंबाई भुजा-भुजा-भुजा मानदंड के अनुसार बराबर होती है, इसलिए त्रिभुज सर्वांगसम होते हैं।
∆ ABC ≅ ∆ DEF
अत: सिद्ध हुआ।
प्रश्न 3. सभी वर्ग ___________ होते हैं। (समरूप, सर्वांगसम)। Most Important
Ans – समरूप
प्रश्न 4. सभी ________ त्रिभुज समरूप होते हैं। ( समद्विबाहु, समबाहु) Most Important
Ans – समबाहु
प्रश्न 5. नीचे त्रिभुज की भुजाएँ दी गई है। इनमें से कौन-सा समकोण त्रिभुज है ? (i) 3 सेमी, 8 सेमी, 6 सेमी (ii) 13 सेमी, 12 सेमी, 5 सेमी
Ans –
एक समकोण त्रिभुज में, कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है (पाइथागोरस प्रमेय)। यानी h2 = p2 + b2, जहां h त्रिभुज की सबसे लंबी भुजा है।
- h2 = 82 = 64
p2 + b2 = 32 + 62 = 45
As, 64 ≠ 45
इसलिए, यह एक समकोण त्रिभुज नहीं है।
- h2 = 132 = 169
p2 + b2 = 122 + 52 = 169
169 = 169
इसलिए, 13 सेमी, 12 सेमी, 5 सेमी भुजाओं वाला त्रिभुज एक समकोण त्रिभुज है।
प्रश्न 6. 90 सेमी की लम्बाई वाली एक लड़की बल्ब लगे एक खंभे के आधार से परे 1.2 मी/से की चाल से चल रही है। यदि बल्ब भूमि से 3.6 मी की ऊँचाई पर है, तो 4 सेकण्ड बाद उस लड़की की छाया की लम्बाई ज्ञात कीजिए।
Ans –
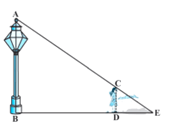
मान लीजिए AB लैंप-पोस्ट को दर्शाता है और लैंप पोस्ट से 4 सेकंड दूर चलने के बाद लड़की को CD दर्शाता है
आकृति से, DE लड़की की छाया है। माना DE x मीटर है।
अब, BD = 1.2 मी. × 4 = 4.8 मी.
∆ ABE और ∆ CDE में,
∠B = ∠D (प्रत्येक 90° का है क्योंकि लैंप-पोस्ट और साथ ही लड़की जमीन पर लंबवत खड़ी है)
∠E = ∠E (समान कोण)
तो, ∆ ABE ~ ∆ CDE (AA समानता मानदंड)
इसलिए,
=
=
( 90cm =
m = 0.9m)
4.8 + x = 4x
3x = 4.8
x = 1.6
तो, 4 सेकंड चलने के बाद लड़की की छाया 1.6 मीटर लंबी है।
प्रश्न 7. आकृति में DE || BC है । BC का मान ज्ञात कीजिए : Most Most Important
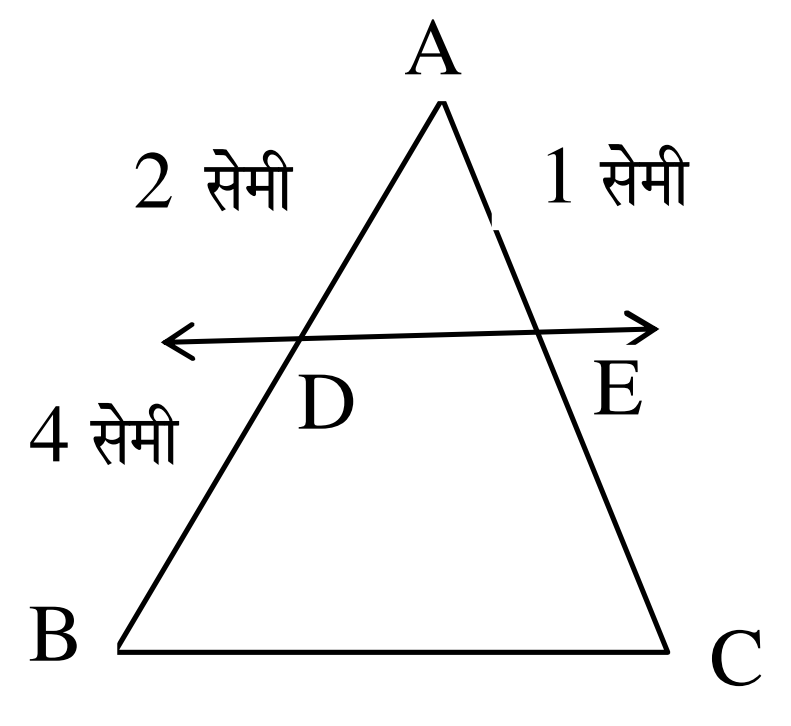
Ans –
आधरभूत समानुपातिकता प्रमेय का उपयोग करते हुए, =
=
EC = 2 cm