NCERT Class 10 Math Chapter 7 Important Question Answer in Hindi – निर्देशांक ज्यामिति

Class 10
Chapter  निर्देशांक ज्यामिति
Subject गणित
Category Important Questions

Class 10 Math Chapter 7 Important Question Answer in Hindi

प्रश्न 1. (-5, 7) और (−1, 3) बिन्दुओं के बीच की दूरी ज्ञात कीजिए। Most Important

Ans – 

बिंदुओं के बीच की दूरी =

= \displaystyle \sqrt{{{{{(-1-(-5))}}^{2}}+{{{(3-7)}}^{2}}}}

= \displaystyle \sqrt{{16+16}} = \displaystyle \sqrt{{32}}

प्रश्न 2. (3, 4) और (4, 7) को मिलाने वाली रेखा को y अक्ष किस अनुपात में विभाजित करता है ? विभाजित करने वाले बिन्दु के निर्देशांक भी ज्ञात कीजिए। Most Important

Ans – 

माना अनुपात k : 1 है। फिर विभाजन सूत्र द्वारा, उस बिंदु के निर्देशांक जो AB को k : 1 के अनुपात में विभाजित करते हैं, \displaystyle \left( {\frac{{-4k+3}}{{k+1}},\frac{{7k+4}}{{k+1}}} \right) हैं

बिंदु y-अक्ष पर स्थित है, और हम जानते हैं कि y-अक्ष पर x-निर्देशांक 0 है।

इसलिए,  \displaystyle \frac{{-4k+3}}{{k+1}} = 0

-4k + 3 = 0

k = \displaystyle \frac{3}{4}

अत: अनुपात 3:4 है। k = \displaystyle \frac{3}{4} का मान रखने पर, हमें प्रतिच्छेदन बिंदु \displaystyle \left( {0,\frac{{37}}{7}} \right) प्राप्त होता है 

प्रश्न 3. बिन्दुओं (a, b) और (-a, -b) के बीच की दूरी ज्ञात कीजिए।

Ans – 

बिंदुओं (x1, y1) और (x2, y2) के बीच की दूरी है

इसलिए, बिंदुओं के बीच की दूरी = \displaystyle \sqrt{{{{{(-a-a)}}^{2}}+{{{(-b-b)}}^{2}}}} = \displaystyle \sqrt{{4{{a}^{2}}+4{{b}^{2}}}} = \displaystyle 2\sqrt{{{{a}^{2}}+{{b}^{2}}}}

प्रश्न 4. यदि रेखाखण्ड का मध्य बिन्दु ( 3, 4) है जिसका एक सिरा (7, – 2) है, तो दूसरे सिरे का निर्देशांक बिन्दु ज्ञात कीजिए।

Ans – 

बिंदुओं से जुड़ने वाले रेखाखंड का मध्य-बिंदु A(x1, y1) और B(x2, y2) हैं

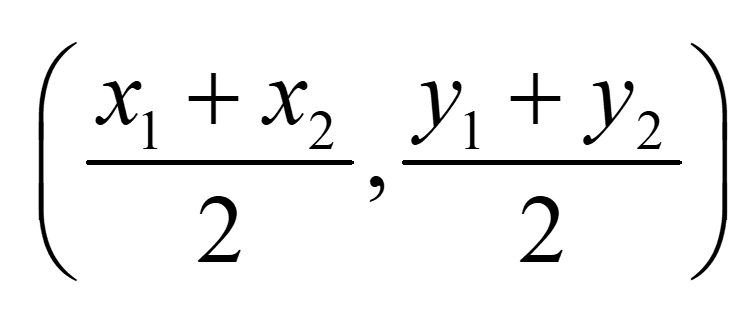
हमे मध्य बिंदु (3, 4) और एक बिंदु (7, -2) के निर्देशांक दिए हैं यानी (x1, y1) और हमें (x2, y2) ढूंढना है

तुलना करने पर,

3 =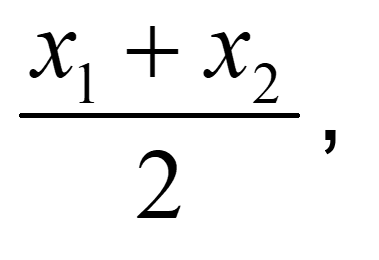  

3 =  \displaystyle \frac{{7+{{x}_{2}}}}{2}

x2 = -1

इसी प्रकार, -2 =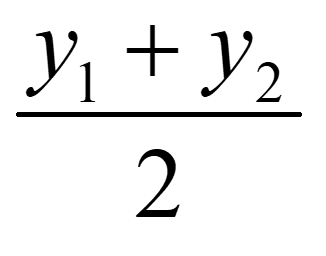

-2 = \displaystyle \frac{{-2+{{y}_{2}}}}{2}

y2 = -2

इसलिए, दूसरे छोर के आवश्यक निर्देशांक (-1, -2) हैं

प्रश्न 5. रेखाखण्ड का मध्यबिन्दु ज्ञात कीजिए जिसके सिरे (4, 5) और (2, −1) हैं।

Ans – 

बिंदुओं से जुड़ने वाले रेखाखंड का मध्य-बिंदु A(x1, y1) और B(x2, y2) हैं

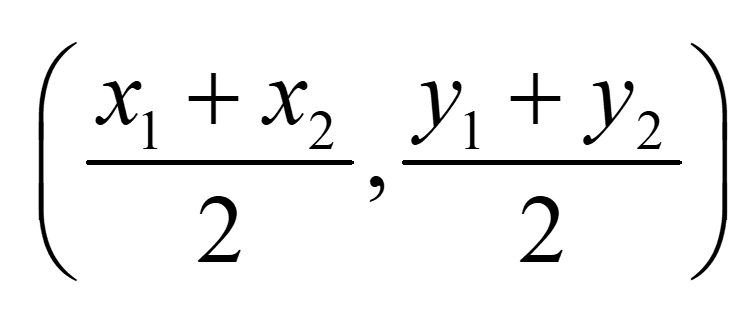
इसलिए, रेखा खंड का मध्य बिंदु (4, 5) और (2, -1) हैं

= \displaystyle \left( {\frac{{4+2}}{2},\frac{{5+(-1)}}{2}} \right)

= (3, 2)

प्रश्न 6. (4, 7) और (2, 3) बिन्दुओं को मिलाने वाली रेखा का मध्य बिन्दु ज्ञात कीजिए।

Ans – 

बिंदुओं से जुड़ने वाले रेखाखंड का मध्य-बिंदु A(x1, y1) और B(x2, y2) हैं

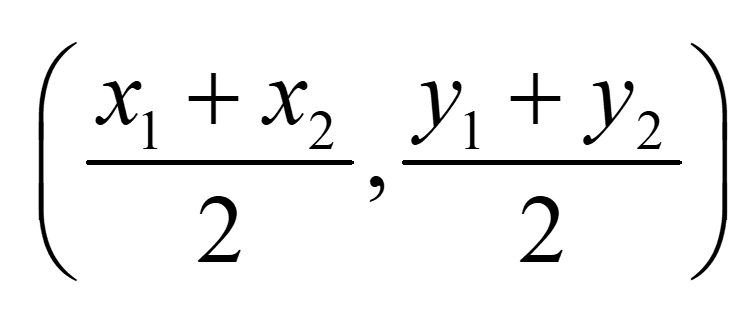
इसलिए, रेखा खंड का मध्य बिंदु (4, 7) और (2, 3) हैं

= \displaystyle \left( {\frac{{4+2}}{2},\frac{{7+3}}{2}} \right)

= (3, 5)

प्रश्न 7. यदि एक रेखाखण्ड का एक सिरा मूल बिन्दु है जिसका मध्य बिन्दु (1, 0) है, दूसरे सिरे का निर्देशांक ज्ञात कीजिए।

Ans – 

बिंदुओं से जुड़ने वाले रेखाखंड का मध्य-बिंदु A(x1, y1) और B(x2, y2) हैं

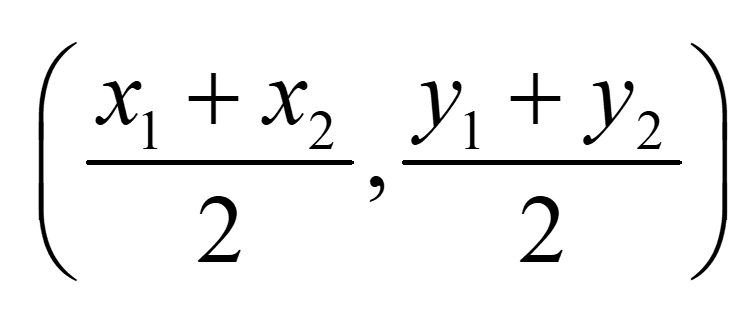
हमे मध्य बिंदु (1, 0) और एक बिंदु (0, 0) के निर्देशांक दिए हैं यानी (x1, y1) और हमें (x2, y2) ढूंढना है

तुलना करने पर,

1=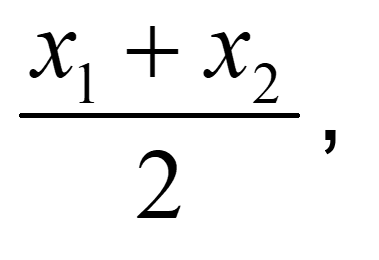

समीकरण में x1 का मान रखने पर हमें प्राप्त होता है,

1 =  \displaystyle \frac{{0+{{x}_{2}}}}{2}

x2 = 2

इसी प्रकार, 0 =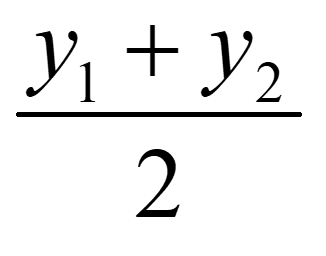

 समीकरण में y1 का मान रखने पर

0 = \displaystyle \frac{{0+{{y}_{2}}}}{2}

y2 = 0

इसलिए, दूसरे छोर के आवश्यक निर्देशांक (2, 0) हैं

प्रश्न 8. बिन्दु A के निर्देशांक ज्ञात कीजिए जहाँ AB एक वृत्त का व्यास है, जिसका केन्द्र (2, -3) है तथा B के निर्देशांक (1, 4) हैं।

Ans – 

बिंदुओं से जुड़ने वाले रेखाखंड का मध्य-बिंदु A(x1, y1) और B(x2, y2) हैं

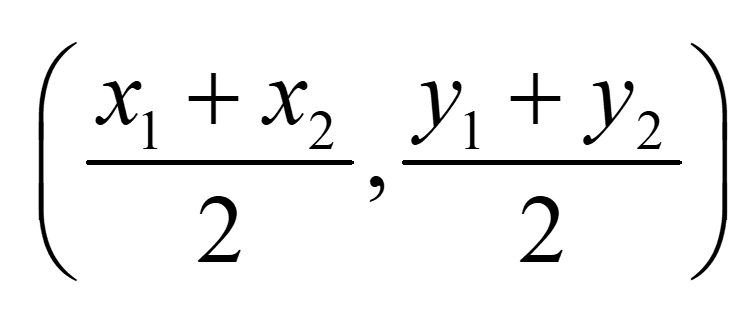
हमे मध्य बिंदु (2, -3) और एक बिंदु B के निर्देशांक (1, 4) दिए हैं और हमें A (x1, y1) ढूंढना है

तुलना करने पर,

2 = \displaystyle \frac{{{{x}_{1}}+1}}{2}

4 = \displaystyle {{x}_{1}}+1

x1 = 3

इसी प्रकार, , -3 = \displaystyle \frac{{{{y}_{1}}+4}}{2}

-6 = \displaystyle {{y}_{1}}+4

Y1 = -10

इसलिए, A के आवश्यक निर्देशांक (3, -10) हैं

प्रश्न 9. यदि बिन्दु A(6, 1), B(8, 2), C(9, 4) और D(p, 3) एक समान्तर चतुर्भुज के शीर्ष इसी क्रम में हो, तो p का मान ज्ञात कीजिए।

Ans – 

हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।

तो, AC के मध्य बिंदु के निर्देशांक = BD के मध्य बिंदु के निर्देशांक

अर्थात 

\displaystyle \left( {\frac{{6+9}}{2},\frac{{1+4}}{2}} \right)=\left( {\frac{{8+p}}{2},\frac{{2+3}}{2}} \right)

\displaystyle \left( {\frac{{15}}{2},\frac{5}{2}} \right)=\left( {\frac{{8+p}}{2},\frac{5}{2}} \right)

\displaystyle \frac{{15}}{2}=\frac{{8+p}}{2}

p = 7

प्रश्न 10. (5, 6) और (-1, -4) को मिलाने वाली रेखा को y-अक्ष किस अनुपात में विभाजित करता है ? विभाजित करने वाले बिन्दु के निर्देशांक भी ज्ञात कीजिए।

Ans – 

माना अनुपात k : 1 है। फिर विभाजन सूत्र द्वारा, उस बिंदु के निर्देशांक जो AB को अनुपात k : 1 में विभाजित करते हैं, \displaystyle \left( {\frac{{-1k+5}}{{k+1}},\frac{{-4k+6}}{{k+1}}} \right) हैं 

यह बिंदु y-अक्ष पर स्थित है, और हम जानते हैं कि y-अक्ष पर x-निर्देशांक 0 है।

इसलिए,  \displaystyle \frac{{-1k+5}}{{k+1}} = 0

-k + 5 = 0

k = 5

अतः अनुपात 5:4 है। k=5 का मान रखने पर, हमें प्रतिच्छेदन बिंदु \displaystyle \left( {0,\frac{{-7}}{3}} \right) मिलता है

प्रश्न 11. बिन्दुओं ( -3, 10) और (6, -8) को जोड़ने वाले रेखाखण्ड को बिन्दु (-1, 6) किस अनुपात में विभाजित करता है, ज्ञात कीजिए।

Ans – 

मान लीजिए कि अनुपात k : 1 है। विभाजन सूत्र का उपयोग करते हुए, हम पाते हैं

(-1, 6) = \displaystyle \left( {\frac{{k(6)+1(-3)}}{{k+1}},\frac{{k(-8)+1(10)}}{{k+1}}} \right)

तो,       -1 = \displaystyle \frac{{6k-3}}{{k+1}}

-k – 1 = 6k – 3

7k = 2

k = \displaystyle \frac{2}{7}

यानी         k : 1 = 2 : 7

तो, बिंदु (-1, 6) बिंदु (-3, 10) और (6, -8) को जोड़ने वाले रेखा खंड को 2 : 7 के अनुपात में विभाजित करता है।

प्रश्न 12. बिन्दुओं A (2, -2) और B(-7, 4) को जोड़ने वाले रेखाखण्ड को सम- त्रिभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।

Ans – 

माना P और Q त्रिखंड AB के बिंदु हैं।

अर्थात AP=PQ=QB

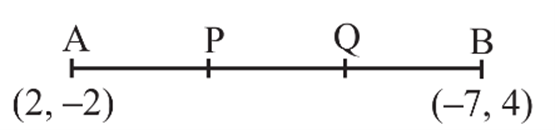
इसलिए, P बिंदु AB को आंतरिक रूप से 1 : 2 के अनुपात में विभाजित करता है। इसलिए, विभाजन सूत्र को लागू करने पर, P के निर्देशांक हैं

\displaystyle \left( {\frac{{1(-7)+2(2)}}{{1+2}},\frac{{1(4)+2(2)}}{{1+2}}} \right)  , यानी (-1, 0)

अब, Q बिंदु भी AB को आंतरिक रूप से 2 : 1 से विभाजित करता है। तो, Q के निर्देशांक हैं

\displaystyle \left( {\frac{{2(-7)+1(2)}}{{2+1}},\frac{{2(4)+1(2)}}{{2+1}}} \right) , यानी, (-4, 2)

प्रश्न 13. बिन्दु (-4, 6), बिन्दुओं ( 6, 10) और B(3, -8) को जोड़ने वाले रेखाखण्ड को किस अनुपात में विभाजित करता है।

Ans – 

माना अनुपात k : 1 हैं। मान लीजिए (-4, 6) AB को आंतरिक रूप से अनुपात k : 1 में विभाजित करता है। विभाजन सूत्र का उपयोग करते हुए, हम पाते हैं

(-4, 6) = \displaystyle \left( {\frac{{3k-6}}{{k+1}},\frac{{-8k+10}}{{k+1}}} \right)

तो,        -4 = \displaystyle \frac{{3k-6}}{{k+1}}

-4k – 4 = 3k – 6

7k = 2

k = \displaystyle \frac{2}{7}

अर्थात           k : 1 = 2 : 7

तो, बिंदु (-4, 6) बिंदु A(-6, 10) और B(3, -8) को जोड़ने वाले रेखा खंड को 2 : 7 के अनुपात में विभाजित करता है।

प्रश्न 14. उस बिन्दु के निर्देशांक, जो बिन्दुओं (4, 3) तथा (8, 5) को जोड़ने वाले रेखाखण्ड को आन्तरिक रूप से 3 : 1 के अनुपात में विभाजित करता हो, है :

Ans – 

माना P(x, y) अभीष्ट बिंदु है। विभाजन सूत्र का उपयोग करते हुए, हम पाते हैं

\displaystyle x=\frac{{3(8)+1(4)}}{{3+1}}=7,

\displaystyle y=\frac{{3(5)+1(-3)}}{{3+1}}=3

इसलिए, (7, 3) अभीष्ट बिंदु है।

Leave a Comment

error: