NCERT Class 10 Math Chapter 7 Important Questions Answer – Coordinate Geometry

Class 10
Chapter  Coordinate Geometry
Subject Math
Category Important Question Answer

Class 10 Math Chapter 7 Important Question Answer

Q1. Find the distance between the points (-5, 7) and (-1, 3). Most Important

Ans. Distance between the points  =

= \displaystyle \sqrt{{{{{(-1-(-5))}}^{2}}+{{{(3-7)}}^{2}}}}

= \displaystyle \sqrt{{16+16}} = \displaystyle \sqrt{{32}}

Q2. Find the ratio in which the line joining (3, 4) and (-4, 7) is divided by y- axis. Also find the coordinates of the point of intersection. Most Important

Ans. Let the ratio be k : 1. Then by the section formula, the coordinates of the point which divides AB in the ratio k : 1 are \displaystyle \left( {\frac{{-4k+3}}{{k+1}},\frac{{7k+4}}{{k+1}}} \right)

The point lies on the y-axis, and we know that on the y-axis the x-coordinate is 0.

Therefore, \displaystyle \frac{{-4k+3}}{{k+1}} = 0

-4k + 3 = 0

k = \displaystyle \frac{3}{4}

Therefore, ratio is 3:4. Putting the value of k = \displaystyle \frac{3}{4} , we get the point of intersection \displaystyle \left( {0,\frac{{37}}{7}} \right)

Q3. Find the distance between points (a, b) and (-a, -b).

Ans. The distance between the points (x1, y1) and (x2, y2) is given by

Therefore,

The distance between the points = \displaystyle \sqrt{{{{{(-a-a)}}^{2}}+{{{(-b-b)}}^{2}}}} = \displaystyle \sqrt{{4{{a}^{2}}+4{{b}^{2}}}} = \displaystyle 2\sqrt{{{{a}^{2}}+{{b}^{2}}}}

Q4. If (3, 4) is mid point of the line segment whose one end is (7, -2), then find the coordinates of the other end point.

Ans. The mid-point of the line segment joining the points  A(x1, y1) and B(x2, y2) are

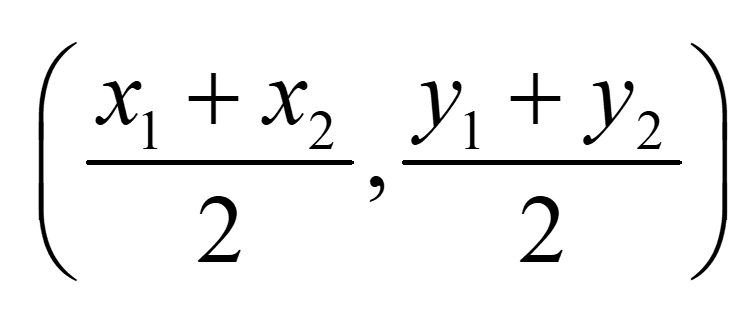
We have given mid points (3, 4) and coordinates of one point (7, -2) i.e ((x1, y1) and we have to find (x2, y2).

On comparing,

3 =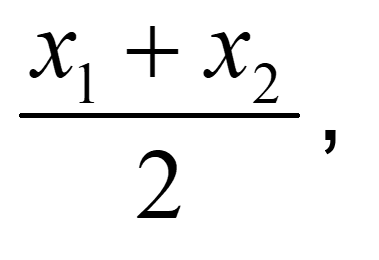  

 

3 =  \displaystyle \frac{{7+{{x}_{2}}}}{2}

x2 = -1

Similarly, -2 =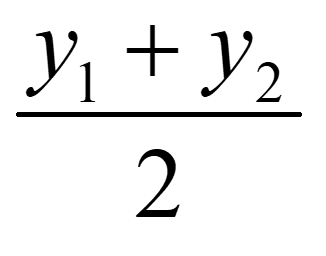

-2 = \displaystyle \frac{{-2+{{y}_{2}}}}{2}

y2 = -2

Therefore, the required coordinates of other end are (-1, -2)

Q5. Find the mid point of the line segment whose end points are (4, 5) and (2, -1).

Ans. The mid-point of the line segment joining the points  A(x1, y1) and B(x2, y2) are

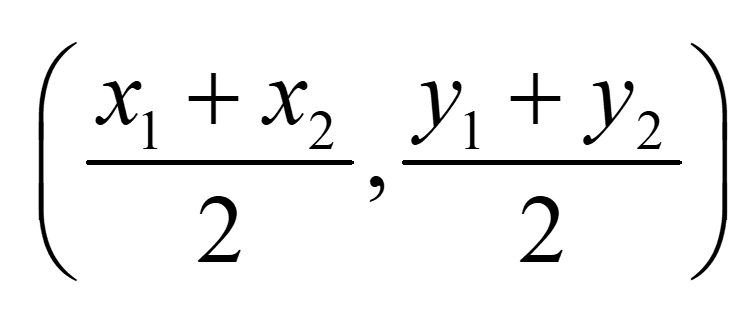
Therefore, the mid point of line segment (4, 5) and (2, -1) are

= \displaystyle \left( {\frac{{4+2}}{2},\frac{{5+(-1)}}{2}} \right)

= (3, 2)

Q6. Find the mid point of the line joining the points (4, 7) and (2, 3).

Ans. The mid-point of the line segment joining the points  A(x1, y1) and B(x2, y2) are

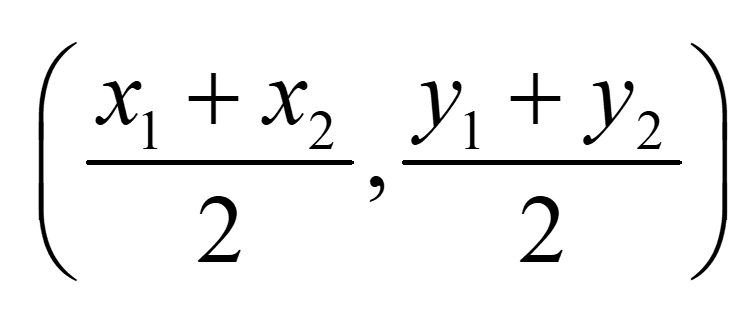
Therefore, the mid point of line segment (4, 7) and (2, 3) are

= \displaystyle \left( {\frac{{4+2}}{2},\frac{{7+3}}{2}} \right)

= (3, 5)

Q7. If origin is at one end of a line segment whose mid point is (1, 0), find the coordinates of other end of segment.

Ans. The mid-point of the line segment joining the points  A(x1, y1) and B(x2, y2) are

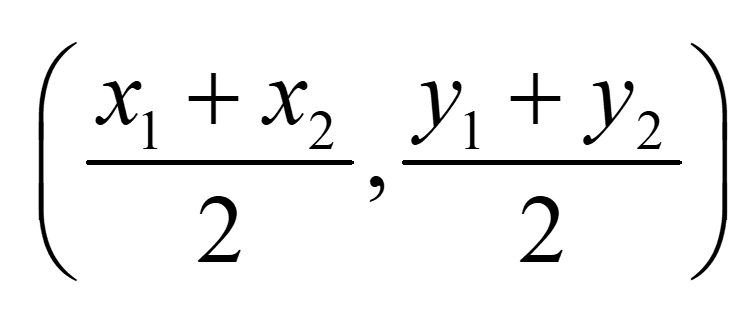
We have given mid points (1, 0) and coordinates of one point at origin means (0, 0) i.e ((x1, y1) and we have to find (x2, y2).

On comparing,

1 =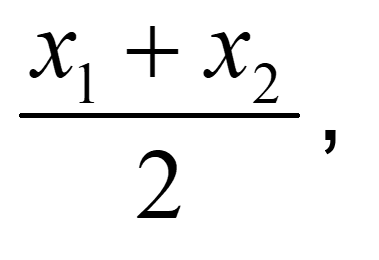

Putting value of x1 in equation we get,

1 =  \displaystyle \frac{{0+{{x}_{2}}}}{2}

x2 = 2

Similarly, 0 =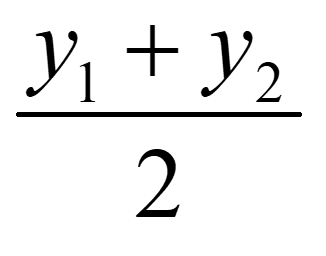

Putting value of y1 in equation,

0 = \displaystyle \frac{{0+{{y}_{2}}}}{2}

y2 = 0

Therefore, the required coordinates of other end are (2, 0)

Q8. Find the co-ordinates of a point A where AB is the diameter of a circle whose centre is (2, -3) and co-ordinates of B is (1, 4).

Ans. The mid-point of the line segment joining the points  A(x1, y1) and B(x2, y2) are

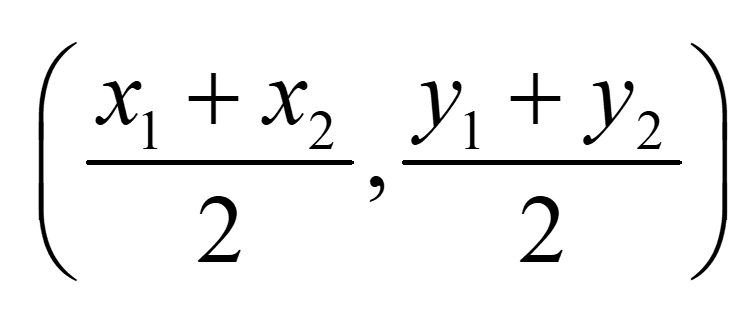
We have given mid points (2, -3) and coordinates B is (1, 4) and we have to find coordinates of A (x1, y1).

On comparing,

2 = \displaystyle \frac{{{{x}_{1}}+1}}{2}

4 = \displaystyle {{x}_{1}}+1

x1 = 3

Similarly, -3 = \displaystyle \frac{{{{y}_{1}}+4}}{2}

-6 = \displaystyle {{y}_{1}}+4

Y1 = -10

Therefore, the required coordinates of A are (3, -10)

Q9. If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.

Ans. We know that diagonals of a parallelogram bisect each other.

So, the coordinates of the mid point of AC = coordinates of the mid-point of BD

i.e.    \displaystyle \left( {\frac{{6+9}}{2},\frac{{1+4}}{2}} \right)=\left( {\frac{{8+p}}{2},\frac{{2+3}}{2}} \right)

\displaystyle \left( {\frac{{15}}{2},\frac{5}{2}} \right)=\left( {\frac{{8+p}}{2},\frac{5}{2}} \right)

so, \displaystyle \frac{{15}}{2}=\frac{{8+p}}{2}

p = 7

Q10. Find the ratio in which the y-axis divides the line segment joining the points (5, 6) and (-1, -4). Also find the point of intersection.

Ans. Let the ratio be k : 1. Then by the section formula, the coordinates of the point which divides AB in the ration k : 1 are \displaystyle \left( {\frac{{-1k+5}}{{k+1}},\frac{{-4k+6}}{{k+1}}} \right)

This point lies on the y-axis, and we know that on the y-axis the x-coordinate is 0.

Therefore, \displaystyle \frac{{-1k+5}}{{k+1}} = 0

-k + 5 = 0

k = 5

Therefore ratio is 5:4. Putting the value of k=5, we get the point of intersection are \displaystyle \left( {0,\frac{{-7}}{3}} \right).

Q11. Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by  (-1, 6).

Ans. Let the ratio k : 1. Using section formula, we get

(-1, 6) = \displaystyle \left( {\frac{{k(6)+1(-3)}}{{k+1}},\frac{{k(-8)+1(10)}}{{k+1}}} \right)

So,        -1 = \displaystyle \frac{{6k-3}}{{k+1}}

-k – 1 = 6k – 3

7k = 2

k = \displaystyle \frac{2}{7}

i.e.      k : 1 = 2 :  7

So, the point (-1, 6) divides the line segment joining the points (-3, 10) and (6, -8) in the ratio 2 : 7.

Q12. Find the co-ordinates of the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4).

Ans. Let P and Q be the points of trisection of AB.

i.e.     AP=PQ=QB

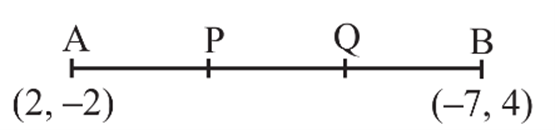
Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordinates of P, by applying the section formula, are

\displaystyle \left( {\frac{{1(-7)+2(2)}}{{1+2}},\frac{{1(4)+2(2)}}{{1+2}}} \right)  , i.e. (-1, 0)

Now, Q also divides AB internally 2:1. So, the coordiates of Q are

\displaystyle \left( {\frac{{2(-7)+1(2)}}{{2+1}},\frac{{2(4)+1(2)}}{{2+1}}} \right)  , i.e.,  (-4, 2)

Q13. In what ratio does the point (-4, 6) divides the line segment joining the points A(-6, 10) and B(3, -8).

Ans. Let the ratio k : 1. Let (-4, 6) divide AB internally in the ratio k : 1. Using the section formula, we get

(-4, 6) = \displaystyle \left( {\frac{{3k-6}}{{k+1}},\frac{{-8k+10}}{{k+1}}} \right)

So,               -4 = \displaystyle \frac{{3k-6}}{{k+1}}

-4k – 4 = 3k – 6

7k = 2

k = \displaystyle \frac{2}{7}

i.e                 k : 1 = 2 : 7

So, the point (-4, 6) divides the line segment joining the points A(-6, 10) and B(3, -8) in the ratio 2 : 7.

[Note : You can check for the y-coordinate also.]

Q14. Find the coordinates of the point which divide the line segment joining the points (4, -3) and (8, 5) in a ratio 3 : 1 internally. Most Important

Ans. Let P(x, y) be the required point. Using the section formula, we get

\displaystyle x=\frac{{3(8)+1(4)}}{{3+1}}=7,

\displaystyle y=\frac{{3(5)+1(-3)}}{{3+1}}=3

Therefore, (7, 3) is the required point.

Also Read Class 10 Math NCERT Solution
Also Read Class 10 Important Questions [Latest]

Leave a Comment

error: