NCERT Class 10 Math Chapter 8 Important Question Answer in Hindi - त्रिकोणमिति का परिचय

Class	10
Chapter	त्रिकोणमिति का परिचय
Subject	गणित
Category	Important Questions

Class 10 Math Chapter 8 Important Question Answer in Hindi

प्रश्न 1. सिद्ध कीजिए : $\displaystyle \frac{{1+\sec A}}{{\sec A}}=\frac{{{{{\sin }}^{2}}A}}{{1- \cos A}}$

Ans –

बाँया पक्ष

$\displaystyle \frac{{1+\sec A}}{{\sec A}}=\frac{{1+\frac{1}{{\cos A}}}}{{\frac{1}{{\cos A}}}}=\left( {\frac{{\cos A+1}}{{\cos A}}} \right)\times \frac{{\cos A}}{1}=1+\cos A$

दाँया पक्ष

$\displaystyle \frac{{{{{\sin }}^{2}}A}}{{1-\cos A}}=\frac{{{{{\sin }}^{2}}A(1+\cos A)}}{{(1-\cos A)(1+\cos A)}}=\frac{{{{{\sin }}^{2}}A(1+\cos A)}}{{1-{{{\cos }}^{2}}A}}$

हम जानते हैं sin²A + cos²A = 1. Therefore, 1 – cos²A = sin²A

$\displaystyle \frac{{{{{\sin }}^{2}}A(1+\cos A)}}{{{{{\sin }}^{2}}A}}=1+\cos A$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 2. सिद्ध कीजिए : $\displaystyle \frac{{\tan \theta }}{{1-\cot \theta }}+\frac{{\cot \theta }}{{1-\tan \theta }}$ = 1 + secθ cosecθ Most Important

Ans –

बाँया पक्ष

$\displaystyle \frac{{\tan \theta }}{{1-\cot \theta }}+\frac{{\cot \theta }}{{1-\tan \theta }}=\frac{{\frac{{\sin \theta }}{{\cos \theta }}}}{{1-\frac{{\cos \theta }}{{\sin \theta }}}}+\frac{{\frac{{\cos \theta }}{{\sin \theta }}}}{{1-\frac{{\sin \theta }}{{\cos \theta }}}}=\frac{{{{{\sin }}^{2}}\theta }}{{\cos \theta (\sin \theta -\cos \theta )}}+\frac{{{{{\cos }}^{2}}\theta }}{{\sin \theta (\cos \theta -\sin \theta )}}$

= $\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{\cos \theta (\sin \theta -\cos \theta )}}-\frac{{{{{\cos }}^{2}}\theta }}{{\sin \theta (\sin \theta -\cos \theta )}}=\frac{{{{{\sin }}^{3}}\theta -{{{\cos }}^{3}}\theta }}{{\sin \theta \cos \theta (\sin \theta -\cos \theta )}}$

हम जानते हैं a³ – b³ = (a – b)(a² + b² + ab)

= $\displaystyle \frac{{(\sin \theta -\cos \theta )({{{\sin }}^{2}}\theta +{{{\cos }}^{2}}\theta +\sin \theta \cos \theta )}}{{\sin \theta \cos \theta (\sin \theta -\cos \theta )}}=\frac{{1+\sin \theta \cos \theta }}{{\sin \theta \cos \theta }}$

दाँया पक्ष

1 + secθ cosecθ = $\displaystyle 1+\frac{1}{{\sin \theta \cos \theta }}=\frac{{\sin \theta \cos \theta +1}}{{\sin \theta \cos \theta }}=\frac{{1+\sin \theta \cos \theta }}{{\sin \theta \cos \theta }}$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 3. सिद्ध कीजिए : (sin A + cosec A)² + (cos A + sec A)² = 7 + tan2A + cot 2A

Ans –

बाँया पक्ष

(sin A + cosec A)² + (cos A + sec A)² = sin²A + cosec²A + 2sinAcosecA + cos²A + sec²A + 2cosAsecA

[As we know sin²A + cos²A = 1, 1 + tan²A = sec²A, 1 + cot²A = cosec²A, $\displaystyle \sin A=\frac{1}{{\cos ecA}},\cos A=\frac{1}{{\sec A}}$ ]

= sin²A + cos²A + cosec²A + 2 + + sec²A + 2

= 1 + 1 + cot²A + 1 + tan²A + 4

= 7 + tan²A + cot²A

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 4. सर्वसमिका cosec²A- cot²A = 1 का प्रयोग करके, सिद्ध कीजिए कि : $\displaystyle \frac{{\cos A+\sin A-1}}{{\cos A-\sin A+1}}=\frac{1}{{\cos ecA+\cot A}}$

Ans –

चूँकि हम cosecA और cotA से संबंधित पहचान लागू करेंगे, आइए पहले अंश और हर को sinA से विभाजित करके बाँया पक्ष को coseA और cotA के रूप में परिवर्तित करें।

बाँया पक्ष

$\displaystyle \frac{{\cos A+\sin A-1}}{{\cos A-\sin A+1}}=\frac{{\cot A+1-\cos ecA}}{{\cot A-1+\cos ecA}}=\frac{{(\cot A-\cos ecA)+1}}{{(\cot A+\cos ecA)-1}}$

= $\displaystyle \frac{{{(\cot A-\cos ecA)+1}(\cot A+\cos ecA)}}{{{(\cot A+\cos ecA)-1}(\cot A+\cos ecA)}}=\frac{{({{{\cot }}^{2}}A-\cos e{{c}^{2}}A)+(\cot A+\cos ecA)}}{{{\cot A+\cos ecA-1}(\cot A+\cos ecA)}}$

= $\displaystyle \frac{{-1+\cot A+\cos ecA}}{{{\cot A+\cos ecA-1}(\cot A+\cos ecA)}}=\frac{{\cot A+\cos ecA-1}}{{{\cot A+\cos ecA-1}(\cot A+\cos ecA)}}$

= $\displaystyle \frac{1}{{\cot A+\cos ecA}}$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 5. सिद्ध कीजिए : $\displaystyle \frac{{\sin \theta +\cos \theta -1}}{{\sin \theta -\cos \theta +1}}=\frac{1}{{\sec \theta +\tan \theta }}$ Most Important

Ans –

चूँकि, दाँया पक्ष में कोण secθ और tanθ में दिए गए हैं, हम बाँया पक्ष के अंश और हर को cosA से विभाजित करके बाँया पक्ष को secθ और tanθ के रूप में परिवर्तित करेंगे।

बाँया पक्ष

$\displaystyle \frac{{\sin \theta +\cos \theta -1}}{{\sin \theta -\cos \theta +1}}=\frac{{\tan \theta +1-\sec \theta }}{{\tan \theta -1+\sec \theta }}=\frac{{(\tan \theta -\sec \theta )+1}}{{(\tan \theta +\sec \theta )-1}}$

= $\displaystyle \frac{{{(\tan \theta -\sec \theta )+1}(\tan \theta +\sec \theta )}}{{{(\tan \theta +\sec \theta )-1}(\tan \theta +\sec \theta )}}=\frac{{({{{\tan }}^{2}}\theta -{{{\sec }}^{2}}\theta )+(\tan \theta +\sec \theta )}}{{{(\tan \theta +\sec \theta )-1}(\tan \theta +\sec \theta )}}$

= $\displaystyle \frac{{-1+\tan \theta +\sec \theta }}{{{\tan \theta +\sec \theta -1}(\tan \theta +\sec \theta )}}=\frac{1}{{\tan \theta +\sec \theta }}$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 6. सिद्ध कीजिए : $\displaystyle \frac{{\cos A-\sin A+1}}{{\cos A+\sin A-1}}=\cos ecA+\cot A$

Ans –

बाँया पक्ष

$\displaystyle \frac{{\cos A-\sin A+1}}{{\cos A+\sin A-1}}=\frac{{\cot A-1+\cos ecA}}{{\cot A+1-\cos ecA}}=\frac{{(\cot A+\cos ecA)-1}}{{(\cot A-\cos ecA)+1}}$

= $\displaystyle \frac{{{(\cot A+\cos ecA)-1}(\cot A-\cos ecA)}}{{{(\cot A-\cos ecA)+1}(\cot A-\cos ecA)}}=\frac{{({{{\cot }}^{2}}A-\cos e{{c}^{2}}A)}}{{{(\cot A-\cos ecA)+1}(\cot A-\cos ecA)}}$

= $\displaystyle \frac{{-1-(\cot A-\cos ecA)}}{{(\cot A-\cos ecA+1)(\cot A-\cos ecA)}}=\frac{{-1(1+\cot A-\cos ecA)}}{{(\cot A-\cos ecA+1)(\cot A-\cos ecA)}}$

= $\displaystyle \frac{{-1}}{{\cot A-\cos ecA}}=\frac{1}{{\cos ecA-\cot A}}=\frac{{\cos ecA+\cot A}}{{(\cos ecA-\cot A)(\cos ecA+\cot A)}}$

= $\displaystyle \frac{{\cos ecA+\cot A}}{{\cos e{{c}^{2}}A-{{{\cot }}^{2}}A}}$ = cosecA + cotA

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 7. सिद्ध कीजिए : $\displaystyle \frac{{\cos \theta }}{{1+\sin \theta }}+\frac{{\cos \theta }}{{1-\sin \theta }}=2\sec \theta$

Ans –

बाँया पक्ष

$\displaystyle \frac{{\cos \theta }}{{1+\sin \theta }}+\frac{{\cos \theta }}{{1-\sin \theta }}=\frac{{\cos \theta (1-\sin \theta )+\cos \theta (1+\sin \theta )}}{{(1+\sin \theta )(1-\sin \theta )}}$

= $\displaystyle \frac{{\cos \theta (1-\sin \theta +1+\sin \theta )}}{{1-{{{\sin }}^{2}}\theta }}=\frac{{2\cos \theta }}{{{{{\cos }}^{2}}\theta }}=\frac{2}{{\cos \theta }}=2\sec \theta$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 8. सिद्ध कीजिए : $\displaystyle \sqrt{{\frac{{1+\sin A}}{{1-\sin A}}}}$ = sec A + tan A

Ans –

बाँया पक्ष

$\displaystyle \sqrt{{\frac{{1+\sin A}}{{1-\sin A}}}}=\sqrt{{\frac{{(1+\sin A)(1+\sin A)}}{{(1-\sin A)(1+\sin A)}}}}=\sqrt{{\frac{{{{{(1+\sin A)}}^{2}}}}{{{{1}^{2}}-{{{\sin }}^{2}}A}}}}=\sqrt{{\frac{{{{{(1+\sin A)}}^{2}}}}{{{{{\cos }}^{2}}A}}}}$

= $\displaystyle \frac{{1+\sin A}}{{\cos A}}=\frac{1}{{\cos A}}+\frac{{\sin A}}{{\cos A}}=\sec A+\tan A$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 9. सिद्ध कीजिए : (cosec θ – cot θ)² = $\displaystyle \frac{{1-\cos \theta }}{{1+\cos \theta }}$

Ans –

बाँया पक्ष

$\displaystyle {{\left( {\cos ec\theta -\cot \theta } \right)}^{2}}=\cos e{{c}^{2}}\theta +{{\cot }^{2}}\theta -2\cos ec\theta \cot \theta$

= $\displaystyle \frac{1}{{{{{\sin }}^{2}}\theta }}+\frac{{{{{\cos }}^{2}}\theta }}{{{{{\sin }}^{2}}\theta }}+\frac{{2\cos \theta }}{{{{{\sin }}^{2}}\theta }}=\frac{{1+{{{\cos }}^{2}}\theta -2\cos \theta }}{{{{{\sin }}^{2}}\theta }}$

दाँया पक्ष

$\displaystyle \frac{{1-\cos \theta }}{{1+\cos \theta }}=\frac{{(1-\cos \theta )(1-\cos \theta )}}{{(1+\cos \theta )(1-\cos \theta )}}=\frac{{1+{{{\cos }}^{2}}\theta -2\cos \theta }}{{{{{\sin }}^{2}}\theta }}$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 10. सिद्ध कीजिए : $\displaystyle \frac{{\cos A}}{{1+\sin A}}+\frac{{1+\sin A}}{{\cos A}}$ = 2sec A

Ans –

बाँया पक्ष

$\displaystyle \frac{{\cos A}}{{1+\sin A}}+\frac{{1+\sin A}}{{\cos A}}=\frac{{\cos A\cos A+(1+\sin A)(1+\sin A)}}{{\cos A(1+\sin A)}}$

= $\displaystyle \frac{{{{{\cos }}^{2}}A+{{{(1+\sin A)}}^{2}}}}{{\cos A(1+\sin A)}}=\frac{{{{{\cos }}^{2}}A+1+{{{\sin }}^{2}}A+2\sin A}}{{\cos A(1+\sin A)}}$

= $\displaystyle \frac{{2+2\sin A}}{{\cos A(1+\sin A)}}=\frac{{2(1+\sin A)}}{{\cos A(1+\sin A)}}=\frac{2}{{\cos A}}=2\sec A$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 11. सिद्ध कीजिए : (cosecA – sinA) (secA – cosA) (tanA + cotA) = 1

Ans –

बाँया पक्ष

= (cosecA – sinA) (secA – cosA) (tanA + cotA)

= $\displaystyle \left( {\frac{1}{{\sin A}}-\sin A} \right)\left( {\frac{1}{{\cos A}}-\cos A} \right)\left( {\frac{{\sin A}}{{\cos A}}+\frac{{\cos A}}{{\sin A}}} \right)$

= $\displaystyle \left( {\frac{{1-{{{\sin }}^{2}}A}}{{\sin A}}} \right)\left( {\frac{{1-{{{\cos }}^{2}}A}}{{\cos A}}} \right)\left( {\frac{{{{{\sin }}^{2}}A+{{{\cos }}^{2}}A}}{{\sin A\cos A}}} \right)$

= $\displaystyle \frac{{{{{\cos }}^{2}}A}}{{\sin A}}\times \frac{{{{{\sin }}^{2}}A}}{{\cos A}}\times \frac{1}{{\sin A\cos A}}$

= 1

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 12. सिद्ध कीजिए : $\displaystyle \frac{{\sin \theta -\cos \theta +1}}{{\sin \theta +\cos \theta -1}}=\frac{1}{{\sec \theta -\tan \theta }}$

Ans –

बाँया पक्ष

$\displaystyle \frac{{\sin -\cos \theta +1}}{{\sin \theta +\cos \theta -1}}=\frac{{\tan -1+\sec \theta }}{{\tan +1-\sec \theta }}=\frac{{(\tan \theta +\sec \theta -1}}{{(\tan \theta -\sec \theta )+1}}$

= $\displaystyle \frac{{{(\tan \theta +\sec \theta )-1}(\tan \theta -\sec \theta )}}{{{(\tan \theta -\sec \theta )+1}(\tan -\sec \theta )}}=\frac{{({{{\tan }}^{2}}\theta -{{{\sec }}^{2}}\theta )-(\tan \theta -\sec \theta )}}{{{\tan \theta -\sec \theta +1}(\tan \theta -\sec \theta )}}$

= $\displaystyle \frac{{-1-\tan \theta +\sec \theta }}{{{\tan \theta -\sec \theta +1}(\tan \theta -\sec \theta )}}=\frac{{-1}}{{\tan \theta -\sec \theta }}$

= $\displaystyle \frac{1}{{\sec \theta -\tan \theta }}$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 13. sin 45° + cos 45° का मान ज्ञात कीजिए। Most Important

Ans – sin 45° + cos 45°= $\displaystyle \frac{1}{{\sqrt{2}}}+\frac{1}{{\sqrt{2}}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$

प्रश्न 14. यदि sin A = $\displaystyle \frac{4}{5}$ , तो cos A का मान ज्ञात कीजिए।

Ans –

SinA = $\displaystyle \frac{P}{H}$ = $\displaystyle \frac{4}{5}$

पाइथागोरस प्रमेय का उपयोग करते हुए, H² = P² + B²

5² = 4² + B²

B² = 9

B = 3

CosA = $\displaystyle \frac{B}{H}$ = $\displaystyle \frac{3}{5}$

प्रश्न 15. tan (A + B) = $\displaystyle \sqrt{3}$ और tan(A – B) = $\displaystyle \frac{1}{{\sqrt{3}}}$ , 0° < A + B ≤ 90°, A > B, तो A और B का मान ज्ञात कीजिए। Most Important

Ans –

जैसा कि हम जानते हैं tan60° = $\displaystyle \sqrt{3}$

इसलिए, A + B = 60° —– (i)

इसी प्रकार, tan30° = $\displaystyle \frac{1}{{\sqrt{3}}}$

इसलिए, A – B = 30° —— (ii)

समीकरण (i) और (ii) जोड़ने पर हमें प्राप्त होता है

2A = 90°

A = 45°

समीकरण (i) में A का मान रखने पर हमें प्राप्त होता है,

B = 15°

प्रश्न 16. यदि sin(A + B) = $\displaystyle \frac{{\sqrt{3}}}{2}$ और sin(A – B) = $\displaystyle \frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, A और B का मान ज्ञात कीजिए।

Ans –

जैसा कि हम जानते हैं sin60° = $\displaystyle \frac{{\sqrt{3}}}{2}$

इसलिए, A + B = 60° —– (i)

इसी प्रकार, sin30° = $\displaystyle \frac{1}{{\sqrt{3}}}$

इसलिए, A – B = 30° —— (ii)

समीकरण (i) और (ii) जोड़ने पर हमें प्राप्त होता है

2A = 90°

A = 45°

समीकरण (i) में A का मान रखने पर हमें प्राप्त होता है,

B = 15°

प्रश्न 17. 1 + tan² θ का मान = __________ होता है।

Ans – sec²θ

प्रश्न 18. $\displaystyle \frac{{2\tan {{{45}}^{\circ }}}}{{1+{{{\tan }}^{2}}{{{45}}^{\circ }}}}$ का मान ज्ञात कीजिए।

Ans –

= $\displaystyle \frac{{2\tan {{{45}}^{o}}}}{{1+{{{\tan }}^{2}}{{{45}}^{o}}}}$ = $\displaystyle \frac{{2(1)}}{{1+{{1}^{2}}}}=\frac{2}{2}=1$

प्रश्न19. सिद्ध कीजिए : $\displaystyle \frac{{\cot A-\cos A}}{{\cot A+\cos A}}=\frac{{\cos ecA-1}}{{\cos ecA+1}}$

Ans –

बाँया पक्ष

$\displaystyle \frac{{\cot A-\cos A}}{{\cot A+\cos A}}=\frac{{\frac{{\cos A}}{{\sin A}}-\cos A}}{{\frac{{\cos A}}{{\sin A}}+\cos A}}$

= $\displaystyle \frac{{\cos A\left( {\frac{1}{{\sin A}}-1} \right)}}{{\cos A\left( {\frac{1}{{\sin A}}+1} \right)}}=\frac{{\left( {\frac{1}{{\sin A}}-1} \right)}}{{\left( {\frac{1}{{\sin A}}+1} \right)}}=\frac{{\cos ecA-1}}{{\cos ecA+1}}$ = RHS

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 20. सिद्ध कीजिए : sec A (1 – sin A) (sec A + tan A) = 1

Ans –

बाँया पक्ष

sec A (1 – sin A) (sec A + tan A) =

= $\displaystyle \frac{{(1-\sin A)(1+\sin A)}}{{{{{\cos }}^{2}}A}}$

= $\displaystyle \frac{{1-{{{\sin }}^{2}}A}}{{{{{\cos }}^{2}}A}}=\frac{{{{{\cos }}^{2}}A}}{{{{{\cos }}^{2}}A}}=1$

बाँया पक्ष = दाँया पक्ष

अत: सिद्ध हुआ

प्रश्न 21. ΔOPQ में, जिसका कोण P समकोण है, OP = 7 cm और OQ – PQ = 1 cm, sin Q और cos Q के मान ज्ञात कीजिए।

Ans –

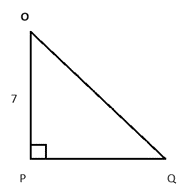
जैसा कि हम जानते हैं, OP = 7cm

मान लीजिए PQ = x cm, then OQ = (x + 1) cm

समकोण ΔOPQ में,

पाइथगोरस प्रमेय का उपयोग करते हुए,

OP² + PQ² = OQ²

7² + x² = (x+1)²

49 + x² = x² + 1 + 2x

48 = 2x

x = 24 cm

PQ = 24 cm, and OQ = 24 + 1 = 25 cm

अब, SinQ = $\displaystyle \frac{{OP}}{{OQ}}=\frac{7}{{25}}$

CosQ = $\displaystyle \frac{{PQ}}{{OQ}}=\frac{{24}}{{25}}$

प्रश्न 22. यदि sin(A-B) = $\displaystyle \frac{1}{2}$ , cos(A+B)= $\displaystyle \frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, तो A और B ज्ञात कीजिए।

Ans –

जैसा कि हम जानते है

sin30^o = $\displaystyle \frac{1}{2}$

इसलिए, A – B = 30 —- (i)

इसी प्रकार, cos60^o = $\displaystyle \frac{1}{2}$

इसलिए, A + B = 60^o —– (ii)

समीकरण (i) और (ii) जोड़ने पर हमें प्राप्त होता है

2A = 90^o

A = 45^o

A का मान समीकरण (ii) में रखने पर हमें प्राप्त होता है

B = 15^o

प्रश्न 23. ΔPQR में, जिसका कोण Q समकोण है, PR + QR = 25 cm और PQ = 5 cm है। sin P का मान ज्ञात कीजिए।

Ans –

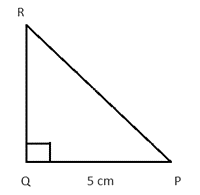
जैसा कि हम जानते है PQ = 5 cm, ΔPQR एक समकोण त्रिभुज है

मान लीजिए PR = x cm,

तब QR = (25 – x) cm

समकोण ΔPQR में,

पाइथागोरस प्रमेय का उपयोग करते हुए,

PQ² + QR² = PR²

5² + (25 – x)² = x²

25 + 625 – 50x + x² = x²

650 = 50x

x = 13 cm

अब, x = PR = 13cm and QR = 25 – x = 25 – 13 = 12 cm

SinP = $\displaystyle \frac{{QR}}{{PR}}=\frac{{12}}{{13}}$

प्रश्न 24. “किसी भी कोण θ के लिए cosθ = $\displaystyle \frac{3}{2}$ ” (सत्य / असत्य)

Ans – असत्य।

चूँकि त्रिभुज का आधार कभी भी कर्ण से बड़ा या उसके बराबर नहीं हो सकता।

इसलिए, cosθ का दिया गया मान गलत है।

प्रश्न 25. “sinθ= cosθ सभी θ के मानों पर” (सत्य / असत्य)

Ans – असत्य

sin0^o ≠ cos0^o

प्रश्न 26. “tanA का मान सदैव -1 और 1 के बीच होता है” (सत्य / असत्य)

Ans – असत्य

चूँकि tanA = $\displaystyle \frac{{\sin A}}{{\cos A}}$ और जब cosA = 0

फिर, tanA को परिभाषित नहीं किया जाएगा।

अतः दिया गया कथन असत्य है।

प्रश्न 27. ” A = 0° पर cot A परिभाषित नहीं है” (सत्य / असत्य)

Ans – सत्य

चूँकि cotA = $\displaystyle \frac{{\cos 0}}{{\sin 0}}$ = परिभाषित नहीं है।

प्रश्न 28. ” secA का मान -1 और 1 के बीच में होता है” (सत्य / असत्य)

Ans – असत्य

कोण 60^o पर sec का मान 2 है जो इस सीमा में नहीं आता है।

प्रश्न 29. “cosec A, cosec और A का गुणनफल है” (सत्य / असत्य)

Ans – असत्य

प्रश्न 30. “cosecθ का मान ≥ 1 और ≤ 1 होता है” (सत्य / असत्य)

Ans – सत्य

प्रश्न 31. ” sinθ = 3/2 किसी भी कोण θ के लिए” (सत्य / असत्य)

Ans – असत्य

क्योंकि लम्ब का मान कभी भी कर्ण से अधिक या उसके बराबर नहीं हो सकता।

प्रश्न 32. मान ज्ञात कीजिए : $\displaystyle \frac{{7{{\sin }}^{2}}{{{30}}^{\circ }}+6\cos e{{c}^{2}} {{{60}}^{\circ }}-{{{\cot }}^{2}}{{{45}}^{\circ }}}}{{{{{\sin }}^{ 2}}{{{60}}^{\circ }}+{{{\cos }}^{2}}{{{60}}^{\circ }}}}$

Ans –

$\displaystyle \frac{{7{{{\left( {\frac{1}{{\sqrt{2}}}} \right)}}^{2}}+6{{{\left( {\frac{2}{{\sqrt{3}}}} \right)}}^{2}}-{{1}^{2}}}}{1}=\frac{7}{4}+8-1=\frac{{35}}{4}$

[sin²θ + cos²θ = 1 का उपयोग करने पर]

प्रश्न 33. मान ज्ञात कीजिए : $\displaystyle \frac{{5{{\cos }}^{2}}{{{60}}^{\circ }}+4{{{\sec }}^{2}} {{{30}}^{\circ }}-{{{\tan }}^{2}}{{{45}}^{\circ }}}}{{{{{\sin }}^{ 2}}{{{30}}^{\circ }}+{{{\cos }}^{2}}{{{30}}^{\circ }}}}$

Ans –

$\displaystyle \frac{{5{{{\left( {\frac{1}{2}} \right)}}^{2}}+4{{{\left( {\frac{2}{{\sqrt{3}}}} \right)}}^{2}}-{{1}^{2}}}}{1}=\frac{5}{4}+\frac{{16}}{3}-1$