NCERT Class 10 Math Chapter 8 Important Questions Answer - Introduction to Trigonometry

Class	10
Chapter	Introduction to Trigonometry
Subject	Math
Category	Important Question Answer

Class 10 Math Chapter 8 Important Question Answer

Q1. Prove that : $\displaystyle \frac{{1+\sec A}}{{\sec A}}=\frac{{{{{\sin }}^{2}}A}}{{1-\cos A}}$

Ans. LHS

$\displaystyle \frac{{1+\sec A}}{{\sec A}}=\frac{{1+\frac{1}{{\cos A}}}}{{\frac{1}{{\cos A}}}}=\left( {\frac{{\cos A+1}}{{\cos A}}} \right)\times \frac{{\cos A}}{1}=1+\cos A$

RHS

$\displaystyle \frac{{{{{\sin }}^{2}}A}}{{1-\cos A}}=\frac{{{{{\sin }}^{2}}A(1+\cos A)}}{{(1-\cos A)(1+\cos A)}}=\frac{{{{{\sin }}^{2}}A(1+\cos A)}}{{1-{{{\cos }}^{2}}A}}$

As we know sin²A + cos²A = 1. Therefore, 1 – cos²A = sin²A

$\displaystyle \frac{{{{{\sin }}^{2}}A(1+\cos A)}}{{{{{\sin }}^{2}}A}}=1+\cos A$

LHS = RHS

Hence proved.

Q2. Prove that : $\displaystyle \frac{{\tan \theta }}{{1-\cot \theta }}+\frac{{\cot \theta }}{{1-\tan \theta }}$ = 1 + secθ cosecθ Most Important

Ans. LHS

$\displaystyle \frac{{\tan \theta }}{{1-\cot \theta }}+\frac{{\cot \theta }}{{1-\tan \theta }}=\frac{{\frac{{\sin \theta }}{{\cos \theta }}}}{{1-\frac{{\cos \theta }}{{\sin \theta }}}}+\frac{{\frac{{\cos \theta }}{{\sin \theta }}}}{{1-\frac{{\sin \theta }}{{\cos \theta }}}}=\frac{{{{{\sin }}^{2}}\theta }}{{\cos \theta (\sin \theta -\cos \theta )}}+\frac{{{{{\cos }}^{2}}\theta }}{{\sin \theta (\cos \theta -\sin \theta )}}$

= $\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{\cos \theta (\sin \theta -\cos \theta )}}-\frac{{{{{\cos }}^{2}}\theta }}{{\sin \theta (\sin \theta -\cos \theta )}}=\frac{{{{{\sin }}^{3}}\theta -{{{\cos }}^{3}}\theta }}{{\sin \theta \cos \theta (\sin \theta -\cos \theta )}}$

Using a³ – b³ = (a – b)(a² + b² + ab)

= $\displaystyle \frac{{(\sin \theta -\cos \theta )({{{\sin }}^{2}}\theta +{{{\cos }}^{2}}\theta +\sin \theta \cos \theta )}}{{\sin \theta \cos \theta (\sin \theta -\cos \theta )}}=\frac{{1+\sin \theta \cos \theta }}{{\sin \theta \cos \theta }}$

RHS

1 + secθ cosecθ = $\displaystyle 1+\frac{1}{{\sin \theta \cos \theta }}=\frac{{\sin \theta \cos \theta +1}}{{\sin \theta \cos \theta }}=\frac{{1+\sin \theta \cos \theta }}{{\sin \theta \cos \theta }}$

LHS = RHS

Hence proved.

Q3. Prove that : (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot²A

Ans. LHS

(sin A + cosec A)² + (cos A + sec A)² = sin²A + cosec²A + 2sinAcosecA + cos²A + sec²A + 2cosAsecA

[As we know sin²A + cos²A = 1, 1 + tan²A = sec²A, 1 + cot²A = cosec²A, $\displaystyle \sin A=\frac{1}{{\cos ecA}},\cos A=\frac{1}{{\sec A}}$ ]

= sin²A + cos²A + cosec²A + 2 + + sec²A + 2

= 1 + 1 + cot²A + 1 + tan²A + 4

= 7 + tan²A + cot²A

LHS = RHS

Hence proved.

Q4. Prove that $\displaystyle \frac{{\cos A+\sin A-1}}{{\cos A-\sin A+1}}=\frac{1}{{\cos ecA+\cot A}}$ , using the identity cosec²A- cot²A = 1.

Ans. Since we will apply the identity involving cosecA and cotA, let us first convert the LHS in terms of coseA and cotA by dividing numerator and denominator by sinA.

LHS

$\displaystyle \frac{{\cos A+\sin A-1}}{{\cos A-\sin A+1}}=\frac{{\cot A+1-\cos ecA}}{{\cot A-1+\cos ecA}}=\frac{{(\cot A-\cos ecA)+1}}{{(\cot A+\cos ecA)-1}}$

= $\displaystyle \frac{{{(\cot A-\cos ecA)+1}(\cot A+\cos ecA)}}{{{(\cot A+\cos ecA)-1}(\cot A+\cos ecA)}}=\frac{{({{{\cot }}^{2}}A-\cos e{{c}^{2}}A)+(\cot A+\cos ecA)}}{{{\cot A+\cos ecA-1}(\cot A+\cos ecA)}}$

= $\displaystyle \frac{{-1+\cot A+\cos ecA}}{{{\cot A+\cos ecA-1}(\cot A+\cos ecA)}}=\frac{{\cot A+\cos ecA-1}}{{{\cot A+\cos ecA-1}(\cot A+\cos ecA)}}$

= $\displaystyle \frac{1}{{\cot A+\cos ecA}}$

LHS = RHS

Hence proved.

Q5. Prove that: $\displaystyle \frac{{\sin \theta +\cos \theta -1}}{{\sin \theta -\cos \theta +1}}=\frac{1}{{\sec \theta +\tan \theta }}$ Most Important

Ans. Since, in RHS angles are given in secθ and tanθ, we will convert the LHS in terms of secθ and tanθ by dividing numerator and denominator of LHS by cosA.

LHS

$\displaystyle \frac{{\sin \theta +\cos \theta -1}}{{\sin \theta -\cos \theta +1}}=\frac{{\tan \theta +1-\sec \theta }}{{\tan \theta -1+\sec \theta }}=\frac{{(\tan \theta -\sec \theta )+1}}{{(\tan \theta +\sec \theta )-1}}$

= $\displaystyle \frac{{{(\tan \theta -\sec \theta )+1}(\tan \theta +\sec \theta )}}{{{(\tan \theta +\sec \theta )-1}(\tan \theta +\sec \theta )}}=\frac{{({{{\tan }}^{2}}\theta -{{{\sec }}^{2}}\theta )+(\tan \theta +\sec \theta )}}{{{(\tan \theta +\sec \theta )-1}(\tan \theta +\sec \theta )}}$

= $\displaystyle \frac{{-1+\tan \theta +\sec \theta }}{{{\tan \theta +\sec \theta -1}(\tan \theta +\sec \theta )}}=\frac{1}{{\tan \theta +\sec \theta }}$

LHS = RHS

Hence proved.

Q6. Prove that: $\displaystyle \frac{{\cos A-\sin A+1}}{{\cos A+\sin A-1}}=\cos ecA+\cot A$

Ans. Since we will apply the identity involving cosecA and cotA, let us first convert the LHS in terms of coseA and cotA by dividing numerator and denominator by sinA.

LHS

$\displaystyle \frac{{\cos A-\sin A+1}}{{\cos A+\sin A-1}}=\frac{{\cot A-1+\cos ecA}}{{\cot A+1-\cos ecA}}=\frac{{(\cot A+\cos ecA)-1}}{{(\cot A-\cos ecA)+1}}$

= $\displaystyle \frac{{{(\cot A+\cos ecA)-1}(\cot A-\cos ecA)}}{{{(\cot A-\cos ecA)+1}(\cot A-\cos ecA)}}=\frac{{({{{\cot }}^{2}}A-\cos e{{c}^{2}}A)}}{{{(\cot A-\cos ecA)+1}(\cot A-\cos ecA)}}$

= $\displaystyle \frac{{-1-(\cot A-\cos ecA)}}{{(\cot A-\cos ecA+1)(\cot A-\cos ecA)}}=\frac{{-1(1+\cot A-\cos ecA)}}{{(\cot A-\cos ecA+1)(\cot A-\cos ecA)}}$

= $\displaystyle \frac{{-1}}{{\cot A-\cos ecA}}=\frac{1}{{\cos ecA-\cot A}}=\frac{{\cos ecA+\cot A}}{{(\cos ecA-\cot A)(\cos ecA+\cot A)}}$

= $\displaystyle \frac{{\cos ecA+\cot A}}{{\cos e{{c}^{2}}A-{{{\cot }}^{2}}A}}$ = cosecA + cotA

LHS = RHS

Hence proved.

Q7. Prove that : $\displaystyle \frac{{\cos \theta }}{{1+\sin \theta }}+\frac{{\cos \theta }}{{1-\sin \theta }}=2\sec \theta$

Ans. LHS

$\displaystyle \frac{{\cos \theta }}{{1+\sin \theta }}+\frac{{\cos \theta }}{{1-\sin \theta }}=\frac{{\cos \theta (1-\sin \theta )+\cos \theta (1+\sin \theta )}}{{(1+\sin \theta )(1-\sin \theta )}}$

= $\displaystyle \frac{{\cos \theta (1-\sin \theta +1+\sin \theta )}}{{1-{{{\sin }}^{2}}\theta }}=\frac{{2\cos \theta }}{{{{{\cos }}^{2}}\theta }}=\frac{2}{{\cos \theta }}=2\sec \theta$

LHS = RHS

Hence proved.

Q8. Prove that : $\displaystyle \sqrt{{\frac{{1+\sin A}}{{1-\sin A}}}}=\sec A+\tan A$

Ans. LHS

$\displaystyle \sqrt{{\frac{{1+\sin A}}{{1-\sin A}}}}=\sqrt{{\frac{{(1+\sin A)(1+\sin A)}}{{(1-\sin A)(1+\sin A)}}}}=\sqrt{{\frac{{{{{(1+\sin A)}}^{2}}}}{{{{1}^{2}}-{{{\sin }}^{2}}A}}}}=\sqrt{{\frac{{{{{(1+\sin A)}}^{2}}}}{{{{{\cos }}^{2}}A}}}}$

= $\displaystyle \frac{{1+\sin A}}{{\cos A}}=\frac{1}{{\cos A}}+\frac{{\sin A}}{{\cos A}}=\sec A+\tan A$

LHS = RHS

Hence proved.

Q9. Prove that: $\displaystyle {{\left( {\cos ec\theta -\cot \theta } \right)}^{2}}=\frac{{1-\cos \theta }}{{1+\cos \theta }}$

Ans. LHS

$\displaystyle {{\left( {\cos ec\theta -\cot \theta } \right)}^{2}}=\cos e{{c}^{2}}\theta +{{\cot }^{2}}\theta -2\cos ec\theta \cot \theta$

= $\displaystyle \frac{1}{{{{{\sin }}^{2}}\theta }}+\frac{{{{{\cos }}^{2}}\theta }}{{{{{\sin }}^{2}}\theta }}+\frac{{2\cos \theta }}{{{{{\sin }}^{2}}\theta }}=\frac{{1+{{{\cos }}^{2}}\theta -2\cos \theta }}{{{{{\sin }}^{2}}\theta }}$

RHS

$\displaystyle \frac{{1-\cos \theta }}{{1+\cos \theta }}=\frac{{(1-\cos \theta )(1-\cos \theta )}}{{(1+\cos \theta )(1-\cos \theta )}}=\frac{{1+{{{\cos }}^{2}}\theta -2\cos \theta }}{{{{{\sin }}^{2}}\theta }}$

LHS = RHS

Hence proved.

Q10. Prove that: $\displaystyle \frac{{\cos A}}{{1+\sin A}}+\frac{{1+\sin A}}{{\cos A}}=2\sec A$

Ans. LHS

$\displaystyle \frac{{\cos A}}{{1+\sin A}}+\frac{{1+\sin A}}{{\cos A}}=\frac{{\cos A\cos A+(1+\sin A)(1+\sin A)}}{{\cos A(1+\sin A)}}$

= $\displaystyle \frac{{{{{\cos }}^{2}}A+{{{(1+\sin A)}}^{2}}}}{{\cos A(1+\sin A)}}=\frac{{{{{\cos }}^{2}}A+1+{{{\sin }}^{2}}A+2\sin A}}{{\cos A(1+\sin A)}}$

= $\displaystyle \frac{{2+2\sin A}}{{\cos A(1+\sin A)}}=\frac{{2(1+\sin A)}}{{\cos A(1+\sin A)}}=\frac{2}{{\cos A}}=2\sec A$

LHS = RHS

Hence proved.

Q11. Prove that: (cosecA – sinA) (secA – cosA) (tanA + cotA) = 1

Ans. LHS

= (cosecA – sinA) (secA – cosA) (tanA + cotA)

= $\displaystyle \left( {\frac{1}{{\sin A}}-\sin A} \right)\left( {\frac{1}{{\cos A}}-\cos A} \right)\left( {\frac{{\sin A}}{{\cos A}}+\frac{{\cos A}}{{\sin A}}} \right)$

= $\displaystyle \left( {\frac{{1-{{{\sin }}^{2}}A}}{{\sin A}}} \right)\left( {\frac{{1-{{{\cos }}^{2}}A}}{{\cos A}}} \right)\left( {\frac{{{{{\sin }}^{2}}A+{{{\cos }}^{2}}A}}{{\sin A\cos A}}} \right)$

= $\displaystyle \frac{{{{{\cos }}^{2}}A}}{{\sin A}}\times \frac{{{{{\sin }}^{2}}A}}{{\cos A}}\times \frac{1}{{\sin A\cos A}}$

= 1

LHS = RHS

Hence proved.

Q12. Prove that : $\displaystyle \frac{{\sin \theta -\cos \theta +1}}{{\sin \theta +\cos \theta -1}}=\frac{1}{{\sec \theta -\tan \theta }}$

Ans. Since, in RHS angles are given in secθ and tanθ, we will convert the LHS in terms of secθ and tanθ by dividing numerator and denominator of LHS by cosA.

LHS

$\displaystyle \frac{{\sin -\cos \theta +1}}{{\sin \theta +\cos \theta -1}}=\frac{{\tan -1+\sec \theta }}{{\tan +1-\sec \theta }}=\frac{{(\tan \theta +\sec \theta -1}}{{(\tan \theta -\sec \theta )+1}}$

= $\displaystyle \frac{{{(\tan \theta +\sec \theta )-1}(\tan \theta -\sec \theta )}}{{{(\tan \theta -\sec \theta )+1}(\tan -\sec \theta )}}=\frac{{({{{\tan }}^{2}}\theta -{{{\sec }}^{2}}\theta )-(\tan \theta -\sec \theta )}}{{{\tan \theta -\sec \theta +1}(\tan \theta -\sec \theta )}}$

= $\displaystyle \frac{{-1-\tan \theta +\sec \theta }}{{{\tan \theta -\sec \theta +1}(\tan \theta -\sec \theta )}}=\frac{{-1}}{{\tan \theta -\sec \theta }}$

= $\displaystyle \frac{1}{{\sec \theta -\tan \theta }}$

LHS = RHS

Hence proved.

Q13. Find the value of sin 45° + cos 45°. Most Important

Ans. sin 45° + cos 45°= $\displaystyle \frac{1}{{\sqrt{2}}}+\frac{1}{{\sqrt{2}}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$

Q14. If sin A = $\displaystyle \frac{4}{5}$ , find the value of cos A.

Ans. SinA = $\displaystyle \frac{P}{H}$ = $\displaystyle \frac{4}{5}$

Using pythagoras theorem, H² = P² + B²

5² = 4² + B²

B² = 9

B = 3

CosA = $\displaystyle \frac{B}{H}$ = $\displaystyle \frac{3}{5}$

Q15. If tan (A + B) = $\displaystyle \sqrt{3}$ and tan(A – B) = $\displaystyle \frac{1}{{\sqrt{3}}}$ , 0° < A + B ≤ 90°, A > B, then find the value of A and B. Most Important

Ans. As we know tan60° = $\displaystyle \sqrt{3}$

Therefore, A + B = 60° —– (i)

Similarly, tan30° = $\displaystyle \frac{1}{{\sqrt{3}}}$

Therefore, A – B = 30° —— (ii)

Adding eq (i) and (ii) we get

2A = 90°

A = 45°

Putting value of A in eq (i) we get,

B = 15°

Q16. If sin(A + B) = $\displaystyle \frac{{\sqrt{3}}}{2}$ and sin(A – B) = $\displaystyle \frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, then find A and B.

Ans. As we know sin60° = $\displaystyle \frac{{\sqrt{3}}}{2}$

Therefore, A + B = 60° —– (i)

Similarly, sin30° = $\displaystyle \frac{1}{{\sqrt{3}}}$

Therefore, A – B = 30° —— (ii)

Adding eq (i) and (ii) we get

2A = 90°

A = 45°

Putting value of A in eq (i) we get,

B = 15°

Q17. The value of 1 + tan² θ = ___________.

Ans. sec²θ

Q18. Find the value of $\displaystyle \frac{{2\tan {{{45}}^{o}}}}{{1+{{{\tan }}^{2}}{{{45}}^{o}}}}$

Ans. = $\displaystyle \frac{{2\tan {{{45}}^{o}}}}{{1+{{{\tan }}^{2}}{{{45}}^{o}}}}$ = $\displaystyle \frac{{2(1)}}{{1+{{1}^{2}}}}=\frac{2}{2}=1$

Q19. Prove that : $\displaystyle \frac{{\cot A-\cos A}}{{\cot A+\cos A}}=\frac{{\cos ecA-1}}{{\cos ecA+1}}$

Ans. LHS

$\displaystyle \frac{{\cot A-\cos A}}{{\cot A+\cos A}}=\frac{{\frac{{\cos A}}{{\sin A}}-\cos A}}{{\frac{{\cos A}}{{\sin A}}+\cos A}}$

= $\displaystyle \frac{{\cos A\left( {\frac{1}{{\sin A}}-1} \right)}}{{\cos A\left( {\frac{1}{{\sin A}}+1} \right)}}=\frac{{\left( {\frac{1}{{\sin A}}-1} \right)}}{{\left( {\frac{1}{{\sin A}}+1} \right)}}=\frac{{\cos ecA-1}}{{\cos ecA+1}}$ = RHS

LHS = RHS

Hence proved.

Q20. Prove that : sec A (1 – sin A) (sec A + tan A) = 1

Ans. LHS

sec A (1 – sin A) (sec A + tan A) =

= $\displaystyle \frac{{(1-\sin A)(1+\sin A)}}{{{{{\cos }}^{2}}A}}$

= $\displaystyle \frac{{1-{{{\sin }}^{2}}A}}{{{{{\cos }}^{2}}A}}=\frac{{{{{\cos }}^{2}}A}}{{{{{\cos }}^{2}}A}}=1$

LHS = RHS

Hence proved.

Q21. In ΔOPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm. Determine the values of sin Q and cos Q.

Ans.

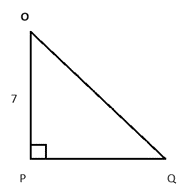
Given, OP = 7cm

Let PQ = x cm, then OQ = (x + 1) cm

In right ΔOPQ,

Using pythgoras theorem,

OP² + PQ² = OQ²

7² + x² = (x+1)²

49 + x² = x² + 1 + 2x

48 = 2x

x = 24 cm

PQ = 24 cm, and OQ = 24 + 1 = 25 cm

Now, SinQ = $\displaystyle \frac{{OP}}{{OQ}}=\frac{7}{{25}}$

CosQ = $\displaystyle \frac{{PQ}}{{OQ}}=\frac{{24}}{{25}}$

Q22. If sin(A-B) = $\displaystyle \frac{1}{2}$ , cos(A+B) = $\displaystyle \frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, find A and B.

Ans. As we know

sin30^o = $\displaystyle \frac{1}{2}$

Therefore, A – B = 30 —- (i)

Similarly, cos60^o = $\displaystyle \frac{1}{2}$

Therefore, A + B = 60^o —– (ii)

Adding eq (i) and (ii) we get

2A = 90^o

A = 45^o

Putting the value of A in eq (ii) we get

B = 15^o

Q23. In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P.

Ans.

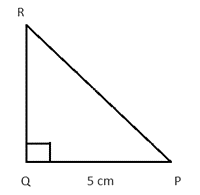
Given, PQ = 5 cm, ΔPQR is a right angled triangle.

Let PR = x cm,

Then QR = (25 – x) cm

In right ΔPQR,

Using pythagoras theorem,

PQ² + QR² = PR²

5² + (25 – x)² = x²

25 + 625 – 50x + x² = x²

650 = 50x

x = 13 cm

Now, x = PR = 13cm and QR = 25 – x = 25 – 13 = 12 cm

SinP = $\displaystyle \frac{{QR}}{{PR}}=\frac{{12}}{{13}}$

Q24. “cosθ = $\displaystyle \frac{3}{2}$ for some angle θ” (true / false)

Ans. As base of triangle can never be greater than or equal to hypotenuse.

Therefore, given value of cosθ is false.

False.

Q25. “sinθ= cosθ for all values of θ” (true / false)

Ans. False.

As sin0^o ≠ cos0^o

Q26. “The value of tanA is always lies in between -1 and 1” (true / false)

Ans. As tanA = $\displaystyle \frac{{\sin A}}{{\cos A}}$ and when cosA = 0

Then, tanA will be not defined.

Hence given statement is false.

Q27. “cotA is not defined for A = 0° ” (true / false)

Ans. True.

As cotA = $\displaystyle \frac{{\cos 0}}{{\sin 0}}$ = not defined.

Q28. “The value of secA is always lies between -1 and 1” (true / false)

Ans. False.

At angle 60^o value of sec is 2 which doesn’t lie in this range.

Q29. “cosec A is the product of cosec and A” (true / false)

Ans. False.

Q30. “The value of cosecθ lies ≥ 1 and ≤ –1 ” (true / false)

Ans. True.

Q31. “sinθ = $\displaystyle \frac{3}{2}$ for some angle θ ” (true / false)

Ans. False.

Because value of perpendicular can never be greater than or equal to hypotenuse.

Q32. Evaluate: $\displaystyle \frac{{7{{{\sin }}^{2}}{{{30}}^{o}}+6\cos e{{c}^{2}}{{{60}}^{o}}-{{{\cot }}^{2}}{{{45}}^{o}}}}{{{{{\sin }}^{2}}{{{60}}^{o}}+{{{\cos }}^{2}}{{{60}}^{o}}}}$

Ans.

$\displaystyle \frac{{7{{{\left( {\frac{1}{{\sqrt{2}}}} \right)}}^{2}}+6{{{\left( {\frac{2}{{\sqrt{3}}}} \right)}}^{2}}-{{1}^{2}}}}{1}=\frac{7}{4}+8-1=\frac{{35}}{4}$

[Using, sin²θ + cos²θ = 1]

Q33. Evaluate: $\displaystyle \frac{{5{{{\cos }}^{2}}{{{60}}^{o}}+4{{{\sec }}^{2}}{{{30}}^{o}}-{{{\tan }}^{2}}{{{45}}^{o}}}}{{{{{\sin }}^{2}}{{{30}}^{o}}+{{{\cos }}^{2}}{{{30}}^{o}}}}$

Ans.

$\displaystyle \frac{{5{{{\left( {\frac{1}{2}} \right)}}^{2}}+4{{{\left( {\frac{2}{{\sqrt{3}}}} \right)}}^{2}}-{{1}^{2}}}}{1}=\frac{5}{4}+\frac{{16}}{3}-1$