| Class | 10 |
| Chapter | त्रिकोणमिति के कुछ अनुप्रयोग |
| Subject | गणित |
| Category | Important Questions |
Class 10 Math Chapter 9 Important Question Answer in Hindi
प्रश्न 1. एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में 40 मी अधिक लम्बी हो जाती है जबकि सूर्य का उन्नयन कोण 60° से घटकर 30° हो जाता है। मीनार की ऊँचाई ज्ञात कीजिए। Most Important
Ans –
मान लीजिए AB मीनार है और BC छाया की लंबाई है, जब सूर्य का उन्नयन कोण 60° है और DB छाया की लंबाई है, जब उन्नयन कोण 30° है।
अब, मान लीजिए AB = h मी., और BC = x मी.
प्रश्न के अनुसार,
DB = (40 + x) मी.

समकोण ∆ ABC में, tan60° =
h = —- (i)
समकोण ∆ ABD में, tan30° =
——- (ii)
समीकरण (i) का मान (ii) में रखने पर हमें मिलता है,
3x = x + 40
2x = 40
x = 20
h =
इसलिए, मीनार की ऊंचाई मी. है।
प्रश्न 2. एक मीनार के पाद बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 मी ऊँची है, तो भवन की ऊँचाई ज्ञात कीजिए।
Ans –
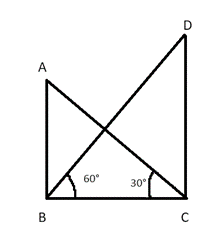
माना AB भवन है और DC मीनार है।
मीनार DC की ऊँचाई DC = 50m,
∠CBD = 60° and ∠BCA = 30°
भवन AB की ऊँचाई = ?
समकोण ∆ DCB में
tan60° =
BC = —- (i)
समकोण ∆ ABC में
tan30° =
BC का मान समीकरण में रखने पर, हमें प्राप्त होता है
3AB = 50
AB =
इसलिए, भवन की ऊंचाई मी. है।
प्रश्न 3. 7 मी ऊँचे एक भवन के शिखर से एक मीनार के शिखर का उन्नयन कोण 60° है और उसके पाद का अवनमन कोण 45° है। मीनार की ऊँचाई ज्ञात कीजिए।
Ans –
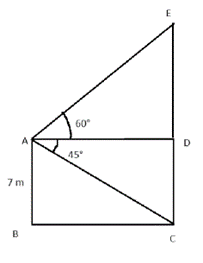
माना भवन की ऊँचाई AB = CD = 7m
∠DAC = ∠BAC = 45° (वैकल्पिक कोण)
साथ ही, ∠DAE = 60°
माना भवन की ऊंचाई EC मी. है
समकोण ∆ ABC में
tan45° =
BC = 7 m
BC = AD
समकोण ∆ ADE में
tan60° =
ED = m
भवन की ऊंचाई EC = ED + DC = + 7 =
m
इसलिए, भवन की ऊंचाई मी. है।
प्रश्न 4. भूमि के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 20 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊंचाई ज्ञात कीजिए।
Ans –
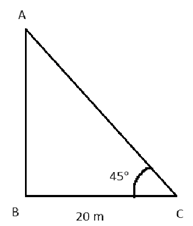
माना मीनार की ऊँचाई AB है।
मीनार के पाद से एक बिंदु की दूरी, BC = 20 m.
टावर के शीर्ष का उन्नयन कोण = 60°
समकोण ∆ ABC में,
tan45° =
AB = 20
इसलिए, मीनार की ऊंचाई 20 मीटर है।
प्रश्न 5. एक पर्यवेक्षक जिसकी लम्बाई 1.6 मी. है। एक मीनार से 20 मी. की दूरी पर है। यदि मीनार की चोटी उसकी आँख पर 60° का कोण बनाती है, तो मीनार की ऊँचाई ज्ञात कीजिए ।
Ans –
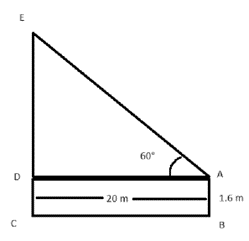
लड़की की ऊँचाई AB = CD = 1.6m,
मीनार और लड़की के बीच की दूरी AD = BC = 20 m
लड़की की आंखों से टावर के शीर्ष का उन्नयन कोण ∠DAE = 60°
चित्र के अनुसार, माना मीनार की ऊंचाई CE मीटर है।
समकोण ∆ ADE में,
tan60° =
DE =
अब, CE = CD + DE = 1.6 +
इसलिए, मीनार की ऊंचाई मीटर है।
प्रश्न 6. धरती पर एक मीनार ऊर्ध्वाधर खड़ी है। धरती के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 15m दूर है, मीनार के शिखर का उन्नयन कोण 60° है। मीनार की ऊंचाई ज्ञात कीजिए।
Ans –
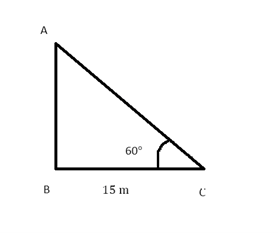
माना मीनार की ऊंचाई AB मी है।
दिया गया है, जमीन से BC एक बिंदु की दूरी, BC = 15 m
मीनार के शीर्ष का उन्नयन कोण 60° है।
समकोण ∆ ABC में,
tan60° =
AB =
इसलिए, मीनार की ऊंचाई मीटर है।
प्रश्न 7. 18 मीटर ऊंचे ऊर्ध्वाधर खंभे से जुड़ा एक तार 24 मीटर लंबा है और दूसरे सिरे पर एक खंभा लगा हुआ है। खंभे के आधार से कितनी दूर तक खंभा गाड़ा जाना चाहिए ताकि तार तना रहे?
Ans –

मान लीजिए कि खंभा BC है और तार की लंबाई AB है। तार को तना हुआ रखने के लिए इसे A पर लगा दें।
तब, ABC C पर समकोण त्रिभुज है।
साथ ही, BC = 18m, AB = 24m.
AC खंभे के आधार से उस बिंदु के बीच की दूरी है।
समकोण ∆ ACB में,
पाइथागोरस प्रमेय का उपयोग करने पर
AB2 = AC2 + BC2
242 = AC2 + 182
576 – 324 = AC2
252 = AC2
AC = m
इसलिए, आवश्यक दूरी मी. है।
प्रश्न 8. एक सीढ़ी किसी दीवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दीवार से 2.5 मीटर की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 मीटर की ऊँचाई पर बनी एक खिड़की तक पहुँचता है। सीढ़ी की लम्बाई ज्ञात कीजिए। Most Important
Ans –

खिड़की AB की ऊँचाई, AB = 6 m
सीढ़ी के पायदान और दीवार BC के बीच की दूरी, BC = 2.5 m
माना सीढ़ी की लंबाई AC मी है।
समकोण ∆ ABC में,
पाइथागोरस प्रमेय का उपयोग करने पर
AB2 + BC2 = AC2
62 + 2.52 = AC2
36 + 6.25 = AC2
AC2 = 42.25
AC = 6.5
इसलिए, सीढ़ी की लंबाई 6.5 मीटर है।
प्रश्न 9. 6 मी० लम्बाई वाले एक ऊर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 4 मी० है जबकि उसी समय एक मीनार की छाया की लम्बाई 28 मी० है मीनार की ऊँचाई ज्ञात कीजिए।
Ans –
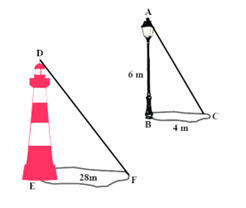
खंभे की ऊंचाई=AB=6 m
खंभे की छाया की लंबाई =BC=4 m
मीनार की छाया की लंबाई=EF=28 m
△ABC और △DEF में
∠B=∠E=90° दोनों 90° क्योंकि दोनों जमीन से लंबवत हैं
∠C=∠F (दोनों मामलों में समान ऊंचाई क्योंकि दोनों छायाएं एक ही समय में पड़ती हैं)
∴△ABC∼△DEF AA समानता मानदंड द्वारा
हम जानते हैं कि यदि दो त्रिभुज समरूप हों तो उनकी भुजाओं का अनुपात समानुपाती होता है
तो,
DE = 6×7 = 42 m
अतः मीनार की ऊंचाई 42 मीटर है।
प्रश्न 10. एक व्यक्ति 10m पूर्व दिशा में चलता है और फिर 30m उत्तर दिशा की ओर चलता है। प्रारंभिक बिन्दु से दूरी ज्ञात कीजिए।
Ans –

माना आरंभ से अंतिम बिंदु तक की दूरी AC है।
दिया गया है AB = 10 m, BC = 30 m.
समकोण ∆ ABC में,
पाइथागोरस प्रमेय का उपयोग करने पर
AB2 + BC2 = AC2
102 + 302 = AC2
1000 = AC2
AC = m.
इसलिए, आवश्यक दूरी मी. है।
प्रश्न 11. पृथ्वी से 15m ऊँचाई पर भवन की एक खिड़की तक 17 m लम्बाई की एक सीढ़ी पहुँचती है। सीढ़ी के पाद से भवन की दूरी ज्ञात कीजिए।
Ans –

सीढ़ी की लंबाई AC = 17m
भवन की ऊँचाई AB = 15 m
माना कि इमारत से सीढ़ी के पायदान की दूरी BC m है।
समकोण ∆ ABC में,
पाइथागोरस प्रमेय का उपयोग करने पर
AB2 + BC2 = AC2
152 + BC2 = 172
289 – 225 = BC2
64 = BC2
BC = 8
इसलिए, इमारत से सीढ़ी के पाद की दूरी 8 मीटर है।
प्रश्न 12. दो खंभे जिसकी ऊँचाईयाँ 6 मी और 12 मी है, एक समतल भूमि पर खड़े हैं। उनके समतल पर पाद की दूरी 8 मी है, तो उनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
Ans –

पहले खंभे AD की ऊँचाई, AD = 6m
दूसरे खंभे की ऊँचाई BE = 12m
दो खंभों के बीच की दूरी AB = DC = 8 m
माना कि खंभों के शीर्षों के बीच की दूरी DE है।
As, AB = DC = 8m
AD = BC = 6m
So, EC = EB – BC = 12 – 6 = 6m
समकोण ∆ DCE में,
पाइथागोरस प्रमेय का उपयोग करने पर
DC2 + EC2 = DE2
82 + 62 = DE2
64 + 36 = DE2
DE = 10
इसलिए, खंभों के ऊपरी सिरों के बीच की दूरी 10 मीटर है।
प्रश्न 13. भूमि के एक बिंदु से एक 20 मी. ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए ।
Ans –
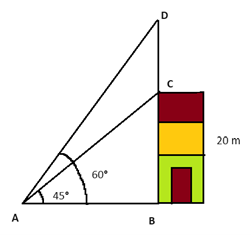
चित्र में, BC भवन की ऊंचाई को दर्शाता है, CD मीनार को और A दिए गए बिंदु को दर्शाता है।
समकोण ∆ ABC पर विचार करते हुए,
AB = 20m
समकोण ∆ ABD में,
BD = m
DC = DB – BC = – 20 =
m
इसलिए, मीनार की ऊंचाई मी. है
प्रश्न 14. एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः 30° और 45° है। यदि पुल किनारों से 3 मीटर की ऊँचाई पर हो, तो नदी की चौड़ाई ज्ञात कीजिए।
Ans –
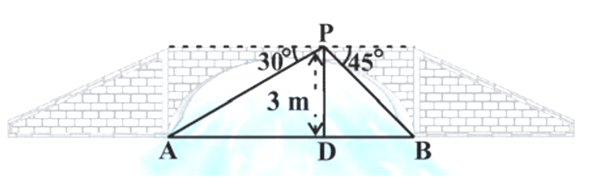
चित्र में, A और B नदी के विपरीत किनारों पर किनारे के बिंदुओं को दर्शाते हैं, ताकि AB नदी की चौड़ाई हो। P पुल पर 3 मीटर की ऊंचाई पर एक बिंदु है, यानी, DP = 3m
नदी की चौड़ाई AB = ?
अब,, AB = AD + DB
समकोण ∆ APD में, ∠A = 30°
tan30° =
AD = m
साथ ही, समकोण ∆ PBD में, ∠B = 45°. So, BD = PD = 3m.
अब, AB = BD + AD = 3 + =
m.
इसलिए, नदी की चौड़ाई मी है।
प्रश्न 15. एक बिजली मिस्त्री को एक 5m ऊँचे खंभे पर आ गई खराबी की मरम्मत करनी है। मरम्मत का काम करने के लिए उसे खंभे के शिखर से 1.3m नीचे एक बिन्दु तक पहुँचने के लिए प्रयुक्त सीढ़ी की लम्बाई कितनी होनी चाहिए जिससे कि जिसे 60° के कोण पर झुकने से वह अपेक्षित स्थिति तक पहुँच जाये और यह भी बताइए कि खंभे का पाद- बिन्दु कितनी दूरी पर सीढ़ी के पाद-बिन्दु से होना चाहिए? ( = 1.73)
Ans –
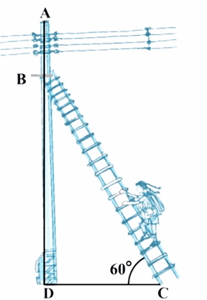
चित्र में, इलेक्ट्रीशियन को खंभे AD पर बिंदु B तक पहुंचना आवश्यक है।
BD = AD – AB = 5 – 1.3 = 3.7 m
यहाँ, BC सीढ़ी को दर्शाता है।
समकोण ∆ BDC में,
(approx.)
अतः सीढ़ी की लंबाई 4.28 मीटर होनी चाहिए।
प्रश्न 16. आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिन्दु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8m है। पेड़ की ऊँचाई ज्ञात कीजिए। Most Important
Ans –

चित्र में, BD पेड़ की ऊंचाई है और बिंदु C से पेड़ टूटकर बिंदु A पर जमीन को छूता है। इसलिए, BD = BC + CD और DC = AC
पेड़ के पैर और उस बिंदु के बीच की दूरी जहां शीर्ष जमीन को छूता है, AB = 8m है
समकोण ∆ ABC में, ∠A = 30°
BC = m
AC = m = CD
BD = BC + CD = m
इसलिए, पेड़ की ऊंचाई (टूटे होने से पहले) मीटर है।
प्रश्न 17. भूमि के बिन्दु P से एक 10 मी ऊँचे भवन के शिखर का उन्नयन कोण 30° है। भवन के शिखर पर एक ध्वज के शिखर का उन्नयन कोण 45° है। ध्वज की लम्बाई और बिन्दु P से भवन की दूरी ज्ञात कीजिए।
Ans –

चित्र में, AB भवन की ऊंचाई को दर्शाता है, BD ध्वज को और P दिए गए बिंदु को दर्शाता है।
BD = ?
समकोण ∆ PAB में,
AP =
P से भवन की दूरी m = 17.32 मीटर है।
अब, मान लीजिए DB = x m. Then AD = (10 + x) m.
समकोण ∆ PAD में,
x = = 7.32
तो, ध्वज की लंबाई 7.32 मीटर है।
प्रश्न 18. 1.2 मी लंबी एक लड़की भूमि से 88.2 मी की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° का है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है। इस अन्तराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए। Most Important
Ans –
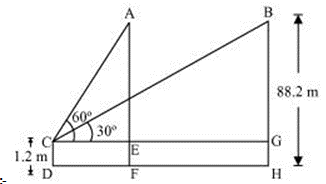
माना CD लड़की है। माना कि गुब्बारे की प्रारंभिक स्थिति A है और कुछ समय बाद दूसरी स्थिति B है।
∆ ACE और ∆ BGC दो समकोण त्रिभुज हैं।
BH = 88.2 मीटर = AF
BG = 88.2 – 1.2 = 87 मीटर = AE
∆ ACE में, tan60° =
m
अब, ∆ BGC में,
EG = m
इसलिए, गुब्बारे द्वारा तय की गई दूरी मीटर है।