NCERT Class 10 Math Chapter 10 Important Questions Answer – Circles

Class	10
Chapter	Circles
Subject	Math
Category	Important Question Answer

---

Class 10 Math Chapter 10 Important Question Answer

---

Q1. The lengths of tangents drawn from an external point to a circle are ___________.

Ans. equal

---

Q2. A circle can have _______ parallel tangents at the most. Most Important

Ans. two

---

Q3. All circles are _________. (Similar/Congruent) Most Important

Ans. similar.

---

Q4. A tangent to a circle intersects it in __________ points. Most Important

Ans. one

---

Q5. A line intersecting a circle in two points is called ___________. Most Important

Ans. Secant

---

Q6. A tangent to a circle intersects it in _________ point(s). 

Ans. one

---

Q7. The common point of a tangent to a circle and the circle is called  __________. Most Important

Ans. point of contact

---

Q8. From a point Q, the length of tangent to a circle is 24 cm and distance of Q from centre is 25 cm. Find the radius of circle.

Ans.

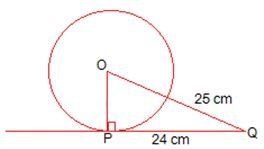
Given, length of tangent PQ = 24 cm

OQ = 25 cm

Radius of Circle OP = ?

As we know, Tangent at any point on the circle is perpendicular to the radius through point of contact

Therefore, OT ⊥ PQ

In ∆ OPQ, Using Pythagoras theorem

OQ² = OP² + PQ²

25² = OP² + 24²

625 – 576 = 49 = OP²

OP = 7 cm

Therefore, length of radius of given circle is 7cm.

---

Q9. Find the length of tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given the radius of circle is 7 cm.

Ans.

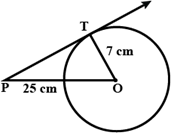
Given, Radius of circle OT = 7 cm

PO = 25 cm

PT = ?

As we know, Tangent at any point on the circle is perpendicular to the radius through point of contact

Therefore, PT ⊥ OT

In ∆ PTO, Using Pythagoras theorem

PO² = TO² + PT²

25² = 7² + PT²

625 – 49 = 576 = PT²

PT = 24 cm

Therefore, required length of tangent is 24 cm.

---

Q10. PQ is a chord of length 8 cm of a circle of radius 5 cm tangents at P and Q intersect at a point T. Find the length TP, if O is the centre of a circle.

Ans.

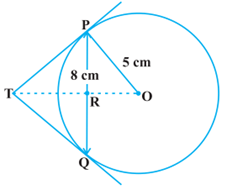
Join OT. Let it intersect PQ at the point R. Then ∆ TPQ is isosceles and TO is the angle bisector of ∠PTQ. So, OT⊥PQ and therefore, OT bisects PQ which gives PR = RQ = 4 cm.

Also, OR = = 3 cm

Now, ∠TPR + ∠RPO = 90° = ∠TPR + ∠PTR

So, ∠RPO = ∠PTR

Therefore, right triangle TRP is similar to the right triangle PRO by AA similarity.

This give,  , i.e.,   or TP = cm.

 

Note : TP can also be found by using pythagoras theorem.

 

Let TP = x and TR = y. Then

Using Pythagoras theorem,

x² = y² + 16  (Taking right ∆ PRT)  —— (i)

x² + 5² = (y + 3)² (Taking right ∆ OPT)  —– (ii)

Subtracting eq (i) from (ii), we get

25 = 6y – 7

y =

putting value of y in eq (i), we get

x² =

x = cm

---

Q11. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Ans.

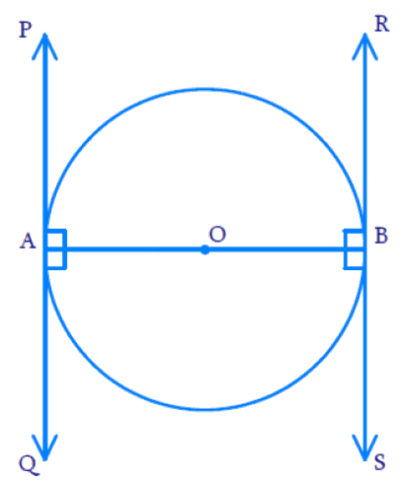
Let us draw a circle with centre O and Diameter AB.

Let two tangents is drawn, one is PQ at point A and other is RS drawn at point B.

As we know,

OA ⊥ PQ (Tangent at any point on the circle is perpendicular to the radius through point of contact)

∠OAP = 90° —– (i)

Similarly, OB ⊥ RS (Tangent at any point on the circle is perpendicular to the radius through point of contact)

∠OBS = 90° —– (ii)

From eq (i) and (ii) we get,

∠OAP = ∠OBS  = 90°

Since, AB is a transversal for lines PQ and RS and ∠BAP = ∠ABS

i.e. If alternate angles are equal then the line are parallel.

Therefore, PQ || RS.

Hence proved.

---

Q12. Prove that the length of tangents drawn from an external point to a circle are equal. Most Most Important

Ans.

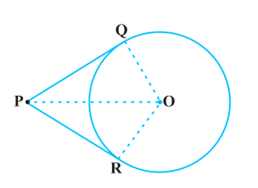
We are given a circle with centre O, a point P lying outside the circle and two tangents PQ, PR on the circle from P.

We are required to prove that PQ = PR.

For this, we join OP, OQ and OR. Then ∠OQP and ∠ORP are right angles, because these are angle between the radii and tangents, and they are right angles as the tangent at any point of a circle is perpendicular to the radius through the point of contact.

Now in right triangles OQP and ORP,

OQ = OR            (Radii of the same circle)

OP = OP            (Common)

Therefore,   OQP ≅ ORP  (RHS)

This gives    PQ = PR   (CPCT)

---

Q13. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠ OPQ.

Ans.

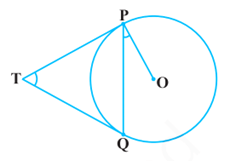
We are given a circle with centre O, an external point T and two tangents TP and TQ to the circle, where P, Q are the point of contact.

We need to prove that

∠PTQ = 2∠OPQ

Let ∠PTQ= θ

Now, TP = TQ as the lengths of tangents drawn from an external path to a circle are equal.

So, TPQ is an isosceles triangle.

Therefore, ∠TPQ = ∠TQP =

Also, ∠OPT = 90^o as the tangent at any point of a circle is perpendicular to the radius through the point of contact.

So, ∠OPQ = ∠OPT – ∠TPQ = 90^o –

=

This gives   ∠PTQ = 2 ∠OPQ

---

Q14. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.

Ans.

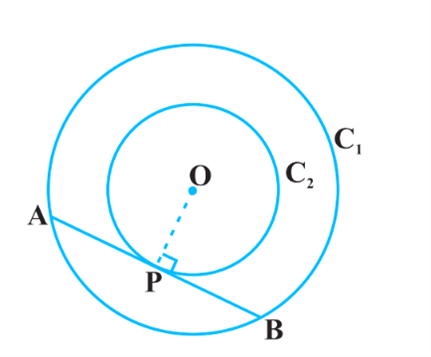
We are given two concentric circles, C₁ and C₂ with centre O and a chord AB of the larger circle C₁ which touches the smaller circle C₂ at the point P.

We need to prove that AP = BP.

Let us join OP.

Then, AB is a tangent to C₂ at P and OP is its radius. Therefore, OP ⊥ AB

Now AB is a chord of the circle C₁ and OP ⊥ AB. Therefore, OP is the bisector of the chord AB, as the perpendicular from the center bisects the chord,

i.e. AP = BP

---

Q15. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Ans.

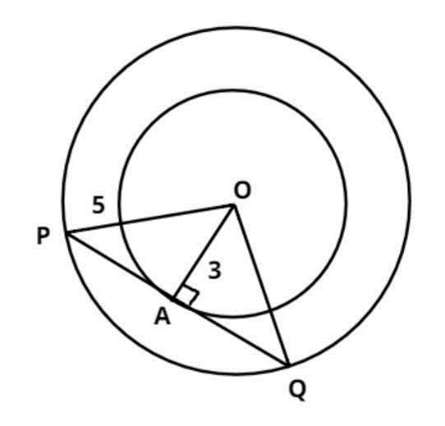
Given radius of bigger circle OP = 5 cm

Radius of smaller circle OA = 3 cm

Find PQ = ?

OA ⊥ PQ (because radius of circle is always perpendicular to its tangent)

Also, PA = AQ (because ∆ OAP ≅ ∆ OAQ)

In ∆ OAP, Using pythagoras theorem,

PO² = PA² + AO²

5² = PA² + 4²

9 = PA²

PA = 3

PQ = PA + AQ = 3 + 3 = 6cm

---

Q16. Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

Ans. Given :  Centre of circle O, PA and PB are tangents drawn at the ends A and B on chord AB.

Prove : ∠PAB  = ∠ PBA

Proof : Join OA and OB.

OA = OB (Radii of the same circle)

∠OAB = ∠OBA (Angles opposite to equal sides) —– (i)

∠OAP = ∠OBP = 90 (As radius is always perpendicular to tangent)

∠OAB + ∠PAB = ∠OBA + ∠PBA  — (ii)

Putting value of eq (i) in eq (ii) we get,

∠OAB + ∠PAB = ∠OAB + ∠PBA

∠PAB =  ∠PBA

Hence proved.

---

Also Read	Class 10 Math NCERT Solution
Also Read	Class 10 Important Questions [Latest]